পাওয়ার সিরিজে ফাংশন সম্প্রসারণ। ফুরিয়ার সিরিজ। ফুরিয়ার সিরিজে একটি ফাংশনের বিস্তার। সাইন এবং কোসাইনগুলির একটি সিরিজে একটি ফাংশনের প্রসারণ

পিরিয়ড 2π সহ পর্যায়ক্রমিক ফাংশনের ফুরিয়ার সিরিজ।

ফুরিয়ার সিরিজ আমাদের পর্যায়ক্রমিক ফাংশনগুলিকে উপাদানগুলিতে পচিয়ে অধ্যয়ন করতে দেয়। বিকল্প স্রোত এবং ভোল্টেজ, স্থানচ্যুতি, ক্র্যাঙ্ক মেকানিজমের গতি এবং ত্বরণ এবং শাব্দ তরঙ্গগুলি ইঞ্জিনিয়ারিং গণনায় পর্যায়ক্রমিক ফাংশনগুলির ব্যবহারের সাধারণ বাস্তব উদাহরণ।

ফুরিয়ার সিরিজের সম্প্রসারণ এই ধারণার উপর ভিত্তি করে যে ব্যবধানে ব্যবহারিক তাত্পর্যের সমস্ত ফাংশন -π ≤x≤ π অভিসারী ত্রিকোণমিতিক সিরিজ আকারে প্রকাশ করা যেতে পারে (একটি ধারা অভিসারী বলে বিবেচিত হয় যদি আংশিক সমষ্টির ক্রম তার পদগুলির সমন্বয়ে গঠিত হয়। একত্রিত হয়):

sinx এবং cosx এর যোগফলের মাধ্যমে স্ট্যান্ডার্ড (=সাধারণ) স্বরলিপি

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...b 1 sinx+b 2 sin2x+b 3 sin3x+...,

যেখানে a o, a 1, a 2,...,b 1, b 2,.. বাস্তব ধ্রুবক, যেমন

যেখানে, -π থেকে π পর্যন্ত সীমার জন্য, ফুরিয়ার সিরিজের সহগগুলি সূত্র ব্যবহার করে গণনা করা হয়:

a o, a n এবং b n সহগগুলিকে বলা হয় ফুরিয়ার সহগ, এবং যদি সেগুলি পাওয়া যায়, তাহলে সিরিজ (1) বলা হয় ফুরিয়ার কাছাকাছি, ফাংশন f(x) এর সাথে সম্পর্কিত। সিরিজ (1) এর জন্য, শব্দটিকে (a 1 cosx+b 1 sinx) বলা হয় প্রথম বা মৌলিক সুরেলা,

একটি সিরিজ লেখার আরেকটি উপায় হল সম্পর্ক ব্যবহার করা acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...c n sin(nx+α n)

যেখানে a o একটি ধ্রুবক, যেখানে 1 =(a 1 2 +b 1 2) 1/2, n =(a n 2 +b n 2) 1/2 সহ - বিভিন্ন উপাদানের প্রশস্ততা, এবং একটি n = arctg এর সমান a n / b n.

সিরিজ (1) এর জন্য, শব্দটি (a 1 cosx+b 1 sinx) বা c 1 sin(x+α 1) বলা হয় প্রথম বা মৌলিক সুরেলা,(a 2 cos2x+b 2 sin2x) বা c 2 sin(2x+α 2) বলা হয় দ্বিতীয় সুরেলাএবং তাই

একটি জটিল সংকেতকে সঠিকভাবে উপস্থাপন করার জন্য সাধারণত অসীম সংখ্যক পদের প্রয়োজন হয়। যাইহোক, অনেক ব্যবহারিক সমস্যায় শুধুমাত্র প্রথম কয়েকটি পদ বিবেচনা করাই যথেষ্ট।

পিরিয়ড 2π সহ অ-পর্যায়ক্রমিক ফাংশনের ফুরিয়ার সিরিজ।

অ-পর্যায়ক্রমিক ফাংশন সম্প্রসারণ.

যদি ফাংশন f(x) অ-পর্যায়ক্রমিক হয়, তাহলে এর অর্থ হল x এর সমস্ত মানের জন্য এটি একটি ফুরিয়ার সিরিজে প্রসারিত করা যাবে না। যাইহোক, 2π প্রস্থের যেকোনো পরিসরের উপর একটি ফাংশনের প্রতিনিধিত্ব করে একটি ফুরিয়ার সিরিজ সংজ্ঞায়িত করা সম্ভব।

একটি অ-পর্যায়ক্রমিক ফাংশন দেওয়া হলে, একটি নির্দিষ্ট সীমার মধ্যে f(x) এর মান নির্বাচন করে এবং 2π ব্যবধানে সেই সীমার বাইরে তাদের পুনরাবৃত্তি করে একটি নতুন ফাংশন তৈরি করা যেতে পারে। যেহেতু নতুন ফাংশনটি পিরিয়ড 2π সহ পর্যায়ক্রমিক, তাই x এর সমস্ত মানের জন্য এটি একটি ফুরিয়ার সিরিজে প্রসারিত করা যেতে পারে। উদাহরণস্বরূপ, ফাংশন f(x)=x পর্যায়ক্রমিক নয়। যাইহোক, যদি এটিকে o থেকে 2π পর্যন্ত ব্যবধানে একটি ফুরিয়ার সিরিজে প্রসারিত করার প্রয়োজন হয়, তবে এই ব্যবধানের বাইরে 2π এর একটি পর্যায়ক্রমিক ফাংশন তৈরি করা হয় (নিচের চিত্রে দেখানো হয়েছে)।

অ-পর্যায়ক্রমিক ফাংশনের জন্য যেমন f(x)=x, ফুরিয়ার সিরিজের যোগফল একটি প্রদত্ত ব্যাপ্তির সমস্ত বিন্দুতে f(x) এর মানের সমান, কিন্তু বিন্দুর জন্য এটি f(x) এর সমান নয় সীমার বাইরে। 2π পরিসরে একটি অ-পর্যায়ক্রমিক ফাংশনের ফুরিয়ার সিরিজ খুঁজে পেতে, ফুরিয়ার সহগগুলির একই সূত্র ব্যবহার করা হয়।

জোড় এবং বিজোড় ফাংশন।

তারা বলে ফাংশন y=f(x) এমনকি, যদি f(-x)=f(x) x এর সকল মানের জন্য। জোড় ফাংশনের গ্রাফ সবসময় y-অক্ষ সম্পর্কে প্রতিসম হয় (অর্থাৎ, তারা মিরর ইমেজ)। জোড় ফাংশনের দুটি উদাহরণ: y=x2 এবং y=cosx।

তারা বলে যে ফাংশন y=f(x) অদ্ভুত x এর সকল মানের জন্য f(-x)=-f(x) হলে। বিজোড় ফাংশনের গ্রাফ সর্বদা উৎপত্তি সম্পর্কে প্রতিসম।

অনেক ফাংশন জোড় বা বিজোড় নয়।

কোসাইনে ফুরিয়ার সিরিজের বিস্তার।

পিরিয়ড 2π সহ একটি জোড় পর্যায়ক্রমিক ফাংশন f(x) এর ফুরিয়ার সিরিজে শুধুমাত্র কোসাইন পদ থাকে (অর্থাৎ কোন সাইন পদ নেই) এবং একটি ধ্রুবক পদ অন্তর্ভুক্ত হতে পারে। তাই,

ফুরিয়ার সিরিজের সহগ কোথায়,

পিরিয়ড 2π সহ একটি বিজোড় পর্যায়ক্রমিক ফাংশন f(x) এর ফুরিয়ার সিরিজে শুধুমাত্র সাইন সহ পদ রয়েছে (অর্থাৎ, এতে কোসাইন সহ পদ নেই)।

তাই,

ফুরিয়ার সিরিজের সহগ কোথায়,

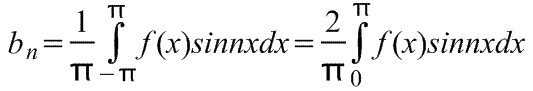
হাফ সাইকেলে ফুরিয়ার সিরিজ।

যদি একটি ফাংশন একটি পরিসরের জন্য সংজ্ঞায়িত করা হয়, বলুন 0 থেকে π পর্যন্ত, এবং শুধুমাত্র 0 থেকে 2π পর্যন্ত নয়, এটি একটি সিরিজে শুধুমাত্র সাইনে বা শুধুমাত্র কোসাইনে প্রসারিত করা যেতে পারে। ফলে ফুরিয়ার সিরিজ বলা হয় হাফ সাইকেলে ফুরিয়ারের কাছে।

আপনি যদি পচন পেতে চান কোসাইন দ্বারা অর্ধ-চক্র ফুরিয়ারফাংশন f(x) 0 থেকে π পর্যন্ত পরিসরে, তারপর একটি জোড় পর্যায়ক্রমিক ফাংশন তৈরি করা প্রয়োজন। চিত্রে। নিচে f(x)=x ফাংশন দেওয়া হল, x=0 থেকে x=π পর্যন্ত ব্যবধানে নির্মিত। যেহেতু এমনকি ফাংশন f(x) অক্ষ সম্পর্কে প্রতিসম, AB রেখা আঁকুন, যেমন চিত্রে দেখানো হয়েছে। নীচে যদি আমরা ধরে নিই যে বিবেচিত ব্যবধানের বাইরে ফলস্বরূপ ত্রিভুজাকার আকৃতিটি পর্যায়ক্রমিক 2π এর সাথে, তাহলে চূড়ান্ত গ্রাফটি এরকম দেখায়: চিত্রে নীচে যেহেতু আমাদের কোসাইনগুলিতে ফুরিয়ার সম্প্রসারণ পেতে হবে, আগের মতো, আমরা ফুরিয়ার সহগ a o এবং a n গণনা করি

যদি পেতে হয় ফুরিয়ার অর্ধ-চক্র সাইন সম্প্রসারণফাংশন f(x) 0 থেকে π পর্যন্ত পরিসরে, তারপর একটি বিজোড় পর্যায়ক্রমিক ফাংশন তৈরি করা প্রয়োজন। চিত্রে। নীচের ফাংশন f(x)=x, x=0 থেকে x=π পর্যন্ত ব্যবধানে নির্মিত। যেহেতু বিজোড় ফাংশন উৎপত্তি সম্পর্কে প্রতিসম, তাই আমরা লাইন সিডি তৈরি করি, যেমনটি চিত্রে দেখানো হয়েছে। যদি আমরা ধরে নিই যে বিবেচিত ব্যবধানের বাইরে ফলস্বরূপ করাত টুথ সংকেতটি 2π এর সময়কালের সাথে পর্যায়ক্রমিক হয়, তাহলে চূড়ান্ত গ্রাফটিতে চিত্রে দেখানো ফর্মটি রয়েছে। যেহেতু আমাদের সাইনের পরিপ্রেক্ষিতে অর্ধ-চক্রের ফুরিয়ার সম্প্রসারণ পেতে হবে, আগের মতো, আমরা ফুরিয়ার সহগ গণনা করি। খ

একটি নির্বিচারে বিরতির জন্য ফুরিয়ার সিরিজ।

পিরিয়ড এল সহ একটি পর্যায়ক্রমিক ফাংশনের প্রসারণ।

পর্যায়ক্রমিক ফাংশন f(x) পুনরাবৃত্তি হয় যখন x L দ্বারা বৃদ্ধি পায়, অর্থাৎ f(x+L)=f(x)। পূর্বে বিবেচিত ফাংশন থেকে 2π এর একটি পিরিয়ডের সাথে ফাংশনে রূপান্তর করা বেশ সহজ, কারণ এটি পরিবর্তনশীল পরিবর্তন ব্যবহার করে করা যেতে পারে।

-L/2≤x≤L/2 রেঞ্জে ফাংশনের ফুরিয়ার সিরিজ খুঁজে পেতে, আমরা একটি নতুন চলক u চালু করি যাতে f(x) ফাংশনের সময়কাল u-এর তুলনায় 2π থাকে। যদি u=2πx/L, তাহলে u=-π এর জন্য x=-L/2 এবং u=π এর জন্য x=L/2। এছাড়াও f(x)=f(Lu/2π)=F(u) দিন। ফুরিয়ার সিরিজ F(u) এর ফর্ম আছে

(একীকরণের সীমা L দৈর্ঘ্যের যেকোনো ব্যবধান দ্বারা প্রতিস্থাপিত হতে পারে, উদাহরণস্বরূপ, 0 থেকে L পর্যন্ত)

ব্যবধান L≠2π-এ নির্দিষ্ট ফাংশনের জন্য অর্ধ-চক্রে ফুরিয়ার সিরিজ।

u=πх/L প্রতিস্থাপনের জন্য, x=0 থেকে x=L পর্যন্ত ব্যবধানটি u=0 থেকে u=π পর্যন্ত ব্যবধানের সাথে মিলে যায়। ফলস্বরূপ, ফাংশনটি শুধুমাত্র কোসাইন বা শুধুমাত্র সাইনে একটি সিরিজে প্রসারিত করা যেতে পারে, যেমন ভি হাফ সাইকেলে ফুরিয়ার সিরিজ.

0 থেকে L পর্যন্ত পরিসরে কোসাইন সম্প্রসারণের ফর্ম আছে

যদি ফাংশন f(x) এর একটি নির্দিষ্ট ব্যবধানে সমস্ত আদেশের ডেরিভেটিভ থাকে a বিন্দু সহ, তাহলে টেলর সূত্রটি এটিতে প্রয়োগ করা যেতে পারে:
,
যেখানে r n– তথাকথিত অবশিষ্ট পদ বা সিরিজের অবশিষ্টাংশ, এটি ল্যাগ্রেঞ্জ সূত্র ব্যবহার করে অনুমান করা যেতে পারে:
, যেখানে x এবং a এর মধ্যে x সংখ্যা।

f(x)=

x 0 বিন্দুতে = সারি উপাদানের সংখ্যা 3 4 5 6 7

পচন ব্যবহার করুন প্রাথমিক ফাংশন e x , cos(x), sin(x), ln(1+x), (1+x) m

ফাংশন প্রবেশের নিয়ম:

যদি কিছু মান জন্য এক্স r n→0 এ n→∞, তারপর সীমার মধ্যে টেলর সূত্রটি এই মানের জন্য একটি অভিসারী সূত্রে পরিণত হয় টেলর সিরিজ:
,
সুতরাং, ফাংশন f(x) বিবেচনাধীন x বিন্দুতে একটি টেলর সিরিজে প্রসারিত করা যেতে পারে যদি:
1) এটিতে সমস্ত আদেশের ডেরিভেটিভ রয়েছে;
2) নির্মিত সিরিজ এই বিন্দুতে একত্রিত হয়।

যখন a = 0 আমরা একটি সিরিজ পাই ম্যাকলরিনের কাছে:
,
Maclaurin সিরিজের সহজতম (প্রাথমিক) ফাংশন সম্প্রসারণ:
সূচকীয় ফাংশন
, আর = ∞
ত্রিকোণমিতিক ফাংশন
, আর = ∞
, আর = ∞
, (-π/2< x < π/2), R=π/2
actgx ফাংশন x এর ক্ষমতায় প্রসারিত হয় না, কারণ ctg0=∞
হাইপারবোলিক ফাংশন


লগারিদমিক ফাংশন
, -1
দ্বিপদী সিরিজ
.

উদাহরণ নং 1। একটি পাওয়ার সিরিজে ফাংশনটি প্রসারিত করুন f(x)= 2x.
সমাধান. ফাংশনের মান এবং এর ডেরিভেটিভগুলি এখানে খুঁজে বের করা যাক এক্স=0
f(x) = 2x, চ( 0) = 2 0 =1;
f"(x) = 2x ln2, চ"( 0) = 2 0 ln2 = ln2;
f""(x) = 2x ln 2 2, চ""( 0) = 2 0 ln 2 2 = ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
ডেরিভেটিভের প্রাপ্ত মানগুলিকে টেলর সিরিজের সূত্রে প্রতিস্থাপন করে, আমরা পাই:

এই সিরিজের কনভারজেন্সের ব্যাসার্ধ অসীমের সমান, তাই এই প্রসারণটি -∞ এর জন্য বৈধ<x<+∞.

উদাহরণ নং 2। ক্ষমতায় টেলর সিরিজ লিখুন ( এক্স+4) ফাংশনের জন্য f(x)= e x.
সমাধান. ফাংশনের ডেরিভেটিভ খুঁজে বের করা e xএবং পয়েন্টে তাদের মান এক্স=-4.
f(x)= ই x, চ(-4) = ই -4 ;
f"(x)= ই x, চ"(-4) = ই -4 ;
f""(x)= ই x, চ""(-4) = ই -4 ;
…
f(n)(x)= ই x, f(n)( -4) = ই -4 .
অতএব, ফাংশনের প্রয়োজনীয় টেলর সিরিজের ফর্ম রয়েছে:

এই সম্প্রসারণটি -∞ এর জন্যও বৈধ<x<+∞.

উদাহরণ নং 3। একটি ফাংশন প্রসারিত করুন f(x)=ln xক্ষমতার একটি সিরিজে ( এক্স- 1),
(অর্থাৎ পয়েন্টের আশেপাশে টেলর সিরিজে এক্স=1).
সমাধান. এই ফাংশনের ডেরিভেটিভগুলি খুঁজুন।
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
এই মানগুলিকে সূত্রে প্রতিস্থাপন করে, আমরা পছন্দসই টেলর সিরিজ পাই:

ডি'আলেমবার্টের পরীক্ষা ব্যবহার করে, আপনি যাচাই করতে পারেন যে সিরিজটি ½x-1½ এ একত্রিত হয়েছে<1 . Действительно,

সিরিজটি ½ হলে একত্রিত হয় এক্স- 1½<1, т.е. при 0<x<2. При এক্স=2 আমরা একটি বিকল্প সিরিজ পাই যা লিবনিজের মানদণ্ডের শর্ত পূরণ করে। যখন x=0 ফাংশন সংজ্ঞায়িত করা হয় না। এইভাবে, টেলর সিরিজের অভিসারণের অঞ্চলটি হল অর্ধ-খোলা ব্যবধান (0;2]।

উদাহরণ নং 4। একটি পাওয়ার সিরিজে ফাংশনটি প্রসারিত করুন।
সমাধান. সম্প্রসারণে (1) আমরা x কে -x 2 দিয়ে প্রতিস্থাপন করি, আমরা পাই:
, -∞

উদাহরণ নং 5। একটি Maclaurin সিরিজে ফাংশন প্রসারিত করুন .
সমাধান. আমরা আছে
সূত্র (4) ব্যবহার করে, আমরা লিখতে পারি:

সূত্রে x এর পরিবর্তে –x প্রতিস্থাপন করলে আমরা পাই:

এখান থেকে আমরা পাই: ln(1+x)-ln(1-x) = -
বন্ধনী খোলা, সিরিজের শর্তাবলী পুনর্বিন্যাস এবং অনুরূপ পদ আনা, আমরা পেতে
. এই সিরিজটি ব্যবধানে একত্রিত হয় (-1;1), যেহেতু এটি দুটি সিরিজ থেকে প্রাপ্ত হয়, যার প্রতিটি এই ব্যবধানে একত্রিত হয়।

মন্তব্য করুন .
সূত্র (1)-(5) একটি টেলর সিরিজে সংশ্লিষ্ট ফাংশন প্রসারিত করতেও ব্যবহার করা যেতে পারে, যেমন ধনাত্মক পূর্ণসংখ্যা শক্তিতে ফাংশন সম্প্রসারণের জন্য ( হা) এটি করার জন্য, একটি ফাংশন (1)-(5) পাওয়ার জন্য একটি প্রদত্ত ফাংশনে এই জাতীয় অভিন্ন রূপান্তরগুলি সম্পাদন করা প্রয়োজন, যার পরিবর্তে এক্সখরচ k( হা) m , যেখানে k একটি ধ্রুবক সংখ্যা, m একটি ধনাত্মক পূর্ণসংখ্যা। পরিবর্তনশীল পরিবর্তন করা প্রায়ই সুবিধাজনক t=হাএবং Maclaurin সিরিজে t এর সাপেক্ষে ফলস্বরূপ ফাংশনটি প্রসারিত করুন।

এই পদ্ধতিটি একটি পাওয়ার সিরিজে একটি ফাংশনের প্রসারণের স্বতন্ত্রতার উপর উপপাদ্যের উপর ভিত্তি করে। এই উপপাদ্যটির সারমর্ম হল যে একই বিন্দুর আশেপাশে দুটি ভিন্ন পাওয়ার সিরিজ পাওয়া যাবে না যা একই ফাংশনে একত্রিত হবে, এটির সম্প্রসারণ যেভাবেই করা হোক না কেন।

উদাহরণ নং 5a. একটি Maclaurin সিরিজে ফাংশন প্রসারিত করুন এবং অভিসারী অঞ্চল নির্দেশ করুন।
সমাধান। প্রথমে আমরা 1-x-6x 2 =(1-3x)(1+2x) , .
প্রাথমিক থেকে:

ভগ্নাংশ 3/(1-3x) 3x এর হর সহ অসীমভাবে হ্রাসপ্রাপ্ত জ্যামিতিক অগ্রগতির সমষ্টি হিসাবে বিবেচনা করা যেতে পারে, যদি |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

অভিসারী অঞ্চলের সাথে |x|< 1/3.

উদাহরণ নং 6। x = 3 বিন্দুর আশেপাশে একটি টেলর সিরিজে ফাংশনটি প্রসারিত করুন।
সমাধান. টেলর সিরিজের সংজ্ঞা ব্যবহার করে এই সমস্যাটি আগের মতোই সমাধান করা যেতে পারে, যার জন্য আমাদের ফাংশনের ডেরিভেটিভ এবং তাদের মান খুঁজে বের করতে হবে এক্স=3। যাইহোক, বিদ্যমান সম্প্রসারণ ব্যবহার করা সহজ হবে (5):
=
ফলে সিরিজটি বা –3 এ একত্রিত হয়

উদাহরণ নং 7। টেলর সিরিজটি ln(x+2) ফাংশনের ক্ষমতা (x -1) এ লিখ।
সমাধান.


সিরিজটি , বা -2 এ একত্রিত হয়< x < 5.

উদাহরণ নং 8। x =2 বিন্দুর আশেপাশে একটি টেলর সিরিজে f(x)=sin(πx/4) ফাংশনটি প্রসারিত করুন।
সমাধান. প্রতিস্থাপন করা যাক t=x-2:

সম্প্রসারণ (3) ব্যবহার করে, যেখানে আমরা x এর জায়গায় π/4 t প্রতিস্থাপন করি, আমরা পাই:

ফলে সিরিজ -∞ এ প্রদত্ত ফাংশনে একত্রিত হয়< π / 4 t<+∞, т.е. при (-∞এইভাবে,
, (-∞

পাওয়ার সিরিজ ব্যবহার করে আনুমানিক গণনা

পাওয়ার সিরিজ আনুমানিক গণনায় ব্যাপকভাবে ব্যবহৃত হয়। তাদের সাহায্যে, আপনি প্রদত্ত নির্ভুলতার সাথে শিকড়, ত্রিকোণমিতিক ফাংশন, সংখ্যার লগারিদম এবং নির্দিষ্ট অখণ্ডগুলির মান গণনা করতে পারেন। ডিফারেনশিয়াল সমীকরণগুলিকে একীভূত করার সময় সিরিজগুলিও ব্যবহৃত হয়।
পাওয়ার সিরিজে একটি ফাংশনের সম্প্রসারণ বিবেচনা করুন:

একটি নির্দিষ্ট পয়েন্টে একটি ফাংশনের আনুমানিক মান গণনা করার জন্য এক্স, নির্দেশিত সিরিজের একত্রিত হওয়ার অঞ্চলের অন্তর্গত, প্রথমগুলি এর সম্প্রসারণে বাকি রয়েছে nসদস্য ( n- একটি সীমিত সংখ্যা), এবং অবশিষ্ট পদগুলি বাতিল করা হয়:

প্রাপ্ত আনুমানিক মানের ত্রুটি অনুমান করার জন্য, বাতিল অবশিষ্ট rn (x) অনুমান করা প্রয়োজন। এটি করার জন্য, নিম্নলিখিত কৌশলগুলি ব্যবহার করুন:

• যদি ফলাফল সিরিজ পর্যায়ক্রমে হয়, তাহলে নিম্নলিখিত বৈশিষ্ট্য ব্যবহার করা হয়: লাইবনিজের শর্ত পূরণকারী একটি বিকল্প সিরিজের জন্য, পরম মূল্যে সিরিজের অবশিষ্টাংশ প্রথম বাতিল করা শব্দের বেশি হয় না.
• যদি প্রদত্ত সিরিজটি ধ্রুবক চিহ্নের হয়, তাহলে বাতিল পদগুলির সমন্বয়ে গঠিত সিরিজটিকে অসীমভাবে হ্রাসপ্রাপ্ত জ্যামিতিক অগ্রগতির সাথে তুলনা করা হয়।
• সাধারণ ক্ষেত্রে, টেলর সিরিজের অবশিষ্টাংশ অনুমান করতে, আপনি ল্যাগ্রেঞ্জ সূত্রটি ব্যবহার করতে পারেন: a x ).

উদাহরণ নং 1। নিকটতম 0.01 এ ln(3) গণনা করুন।
সমাধান. আসুন সম্প্রসারণটি ব্যবহার করি যেখানে x=1/2 (আগের বিষয়ের উদাহরণ 5 দেখুন):

এটি করার জন্য আমরা সীমাহীনভাবে হ্রাসপ্রাপ্ত জ্যামিতিক অগ্রগতির যোগফল ব্যবহার করে এটিকে মূল্যায়ন করব।

তাই আমরা এই অবশিষ্টাংশ বাতিল এবং পেতে পারেন

উদাহরণ নং 2। নিকটতম 0.0001 গণনা করুন।
সমাধান. চলুন দ্বিপদী সিরিজ ব্যবহার করা যাক। যেহেতু 5 3 হল 130 এর কাছাকাছি একটি পূর্ণসংখ্যার ঘনক, তাই 130 সংখ্যাটিকে 130 = 5 3 +5 হিসাবে উপস্থাপন করা যুক্তিযুক্ত।



যেহেতু ইতিমধ্যেই লাইবনিজের মানদণ্ডকে সন্তুষ্ট করে ফলে বিকল্প সিরিজের চতুর্থ মেয়াদটি প্রয়োজনীয় নির্ভুলতার চেয়ে কম:
, তাই এটি এবং এটি অনুসরণ করা শর্তাবলী বাতিল করা যেতে পারে।
নিউটন-লাইবনিজ সূত্র ব্যবহার করে ব্যবহারিকভাবে প্রয়োজনীয় অনেক নির্দিষ্ট বা অনুপযুক্ত অখণ্ডের গণনা করা যায় না, কারণ এর প্রয়োগ অ্যান্টিডেরিভেটিভ খোঁজার সাথে জড়িত, যার প্রায়শই প্রাথমিক ফাংশনে কোনো অভিব্যক্তি থাকে না। এটিও ঘটে যে একটি অ্যান্টিডেরিভেটিভ খুঁজে পাওয়া সম্ভব, তবে এটি অপ্রয়োজনীয়ভাবে শ্রম-নিবিড়। যাইহোক, যদি ইন্টিগ্র্যান্ড ফাংশনকে একটি পাওয়ার সিরিজে প্রসারিত করা হয় এবং ইন্টিগ্রেশনের সীমাগুলি এই সিরিজের কনভারজেন্সের ব্যবধানের অন্তর্গত হয়, তাহলে পূর্বনির্ধারিত নির্ভুলতার সাথে ইন্টিগ্র্যালের একটি আনুমানিক গণনা সম্ভব।

উদাহরণ নং 3। অখণ্ড ∫ 0 1 4 sin (x) x থেকে 10 -5 এর মধ্যে গণনা করুন।
সমাধান. সংশ্লিষ্ট অনির্দিষ্ট অবিচ্ছেদ্য প্রাথমিক ফাংশনে প্রকাশ করা যায় না, যেমন একটি "অ-স্থায়ী অবিচ্ছেদ্য" প্রতিনিধিত্ব করে। নিউটন-লাইবনিজ সূত্র এখানে প্রয়োগ করা যাবে না। চলুন আনুমানিক অবিচ্ছেদ্য গণনা করা যাক।
পাপের জন্য ধারাকে পদ দ্বারা বিভক্ত করা xঅন x, আমরা পাই:

এই সিরিজ টার্মটি টার্ম অনুসারে একীভূত করা (এটি সম্ভব, যেহেতু ইন্টিগ্রেশনের সীমা এই সিরিজের কনভারজেন্সের ব্যবধানের অন্তর্গত), আমরা পাই:

যেহেতু ফলাফলের সিরিজ লিবনিজের শর্তগুলিকে সন্তুষ্ট করে এবং প্রদত্ত নির্ভুলতার সাথে পছন্দসই মান পেতে প্রথম দুটি পদের যোগফল নেওয়া যথেষ্ট।
এইভাবে, আমরা খুঁজে পাই
.

উদাহরণ নং 4। 0.001 এর নির্ভুলতার সাথে অবিচ্ছেদ্য ∫ 0 1 4 e x 2 গণনা করুন।
সমাধান.
. আসুন আমরা ফলাফল সিরিজের দ্বিতীয় মেয়াদের পরে অবশিষ্টটি বাতিল করতে পারি কিনা তা পরীক্ষা করে দেখি।
0.0001<0.001. Следовательно, .

যদি ফাংশন f(x)বিন্দু ধারণকারী কিছু ব্যবধান আছে ক, সমস্ত আদেশের ডেরিভেটিভস, তারপর টেলর সূত্র এটিতে প্রয়োগ করা যেতে পারে:

যেখানে r n– তথাকথিত অবশিষ্ট পদ বা সিরিজের অবশিষ্টাংশ, এটি ল্যাগ্রেঞ্জ সূত্র ব্যবহার করে অনুমান করা যেতে পারে:

, যেখানে x সংখ্যার মধ্যে আছে এক্সএবং ক.

যদি কিছু মান জন্য x r n®0 এ n®¥, তারপর সীমার মধ্যে টেলর সূত্রটি এই মানের জন্য একটি অভিসারী সূত্রে পরিণত হয় টেলর সিরিজ:

তাই ফাংশন f(x)প্রশ্নবিন্দুতে একটি টেলর সিরিজে প্রসারিত করা যেতে পারে এক্স, যদি:

1) এটিতে সমস্ত আদেশের ডেরিভেটিভ রয়েছে;

2) নির্মিত সিরিজ এই বিন্দুতে একত্রিত হয়।

এ ক=0 আমরা নামক একটি সিরিজ পাই ম্যাকলরিনের কাছে:

উদাহরণ 1 f(x)= 2x.

সমাধান. ফাংশনের মান এবং এর ডেরিভেটিভগুলি এখানে খুঁজে বের করা যাক এক্স=0

f(x) = 2x, চ( 0) = 2 0 =1;

f¢(x) = 2x ln2, f¢( 0) = 2 0 ln2 = ln2;

f¢(x) = 2x ln 2 2, চ¢( 0) = 2 0 ln 2 2 = ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.

ডেরিভেটিভের প্রাপ্ত মানগুলিকে টেলর সিরিজের সূত্রে প্রতিস্থাপন করে, আমরা পাই:

এই সিরিজের কনভারজেন্সের ব্যাসার্ধ অসীমের সমান, তাই এই সম্প্রসারণ -¥ এর জন্য বৈধ<x<+¥.

উদাহরণ 2 এক্স+4) ফাংশনের জন্য f(x)= e x.

সমাধান. ফাংশনের ডেরিভেটিভ খুঁজে বের করা e xএবং পয়েন্টে তাদের মান এক্স=-4.

f(x)= ই x, চ(-4) = ই -4 ;

f¢(x)= ই x, f¢(-4) = ই -4 ;

f¢(x)= ই x, চ¢(-4) = ই -4 ;

f(n)(x)= ই x, f(n)( -4) = ই -4 .

অতএব, ফাংশনের প্রয়োজনীয় টেলর সিরিজের ফর্ম রয়েছে:

এই সম্প্রসারণ -¥ এর জন্যও বৈধ<x<+¥.

উদাহরণ 3 . একটি ফাংশন প্রসারিত করুন f(x)=ln xক্ষমতার একটি সিরিজে ( এক্স- 1),

(অর্থাৎ পয়েন্টের আশেপাশে টেলর সিরিজে এক্স=1).

সমাধান. এই ফাংশনের ডেরিভেটিভগুলি খুঁজুন।

এই মানগুলিকে সূত্রে প্রতিস্থাপন করে, আমরা পছন্দসই টেলর সিরিজ পাই:

ডি'আলেমবার্টের পরীক্ষা ব্যবহার করে, আপনি যাচাই করতে পারেন যে সিরিজটি কখন একত্রিত হয়

½ এক্স- 1½<1. Действительно,

সিরিজটি ½ হলে একত্রিত হয় এক্স- 1½<1, т.е. при 0<x<2. При এক্স=2 আমরা একটি বিকল্প সিরিজ পাই যা লিবনিজের মানদণ্ডের শর্ত পূরণ করে। এ এক্স=0 ফাংশন সংজ্ঞায়িত করা হয় না। এইভাবে, টেলর সিরিজের অভিসারণের অঞ্চলটি হল অর্ধ-খোলা ব্যবধান (0;2]।

আসুন ম্যাকলরিন সিরিজে (অর্থাৎ বিন্দুর আশেপাশে) এইভাবে প্রাপ্ত বিস্তৃতিগুলি উপস্থাপন করি এক্স=0) কিছু প্রাথমিক ফাংশনের জন্য:

(2) ,

(3) ,

(শেষ পচন বলা হয় দ্বিপদী সিরিজ)

উদাহরণ 4 . একটি পাওয়ার সিরিজে ফাংশনটি প্রসারিত করুন

সমাধান. সম্প্রসারণে (1) আমরা প্রতিস্থাপন করি এক্সঅন ​​- এক্স 2, আমরা পাই:

উদাহরণ 5 . একটি Maclaurin সিরিজে ফাংশন প্রসারিত করুন

সমাধান. আমরা আছে

সূত্র (4) ব্যবহার করে, আমরা লিখতে পারি:

পরিবর্তে প্রতিস্থাপন এক্সসূত্রের মধ্যে -এক্স, আমরা পাই:

এখান থেকে আমরা খুঁজে পাই:

বন্ধনী খোলা, সিরিজের শর্তাবলী পুনর্বিন্যাস এবং অনুরূপ পদ আনা, আমরা পেতে

এই সিরিজ বিরতিতে একত্রিত হয়

(-1;1), যেহেতু এটি দুটি সিরিজ থেকে প্রাপ্ত হয়, যার প্রতিটি এই ব্যবধানে একত্রিত হয়।

মন্তব্য করুন .

সূত্র (1)-(5) একটি টেলর সিরিজে সংশ্লিষ্ট ফাংশন প্রসারিত করতেও ব্যবহার করা যেতে পারে, যেমন ধনাত্মক পূর্ণসংখ্যা শক্তিতে ফাংশন সম্প্রসারণের জন্য ( হা) এটি করার জন্য, একটি ফাংশন (1)-(5) পাওয়ার জন্য একটি প্রদত্ত ফাংশনে এই জাতীয় অভিন্ন রূপান্তরগুলি সম্পাদন করা প্রয়োজন, যার পরিবর্তে এক্সখরচ k( হা) m , যেখানে k একটি ধ্রুবক সংখ্যা, m একটি ধনাত্মক পূর্ণসংখ্যা। পরিবর্তনশীল পরিবর্তন করা প্রায়ই সুবিধাজনক t=হাএবং Maclaurin সিরিজে t এর সাপেক্ষে ফলস্বরূপ ফাংশনটি প্রসারিত করুন।

এই পদ্ধতিটি একটি ফাংশনের পাওয়ার সিরিজ সম্প্রসারণের স্বতন্ত্রতার উপর উপপাদ্যকে চিত্রিত করে। এই উপপাদ্যটির সারমর্ম হল যে একই বিন্দুর আশেপাশে দুটি ভিন্ন পাওয়ার সিরিজ পাওয়া যাবে না যা একই ফাংশনে একত্রিত হবে, এটির সম্প্রসারণ যেভাবেই করা হোক না কেন।

উদাহরণ 6 . একটি বিন্দুর আশেপাশে একটি টেলর সিরিজে ফাংশন প্রসারিত করুন এক্স=3.

সমাধান. টেলর সিরিজের সংজ্ঞা ব্যবহার করে এই সমস্যাটি আগের মতোই সমাধান করা যেতে পারে, যার জন্য আমাদের ফাংশনের ডেরিভেটিভ এবং তাদের মান খুঁজে বের করতে হবে এক্স=3। যাইহোক, বিদ্যমান সম্প্রসারণ ব্যবহার করা সহজ হবে (5):

ফলে সিরিজ এ একত্রিত হয় অথবা -3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

উদাহরণ 7 . ক্ষমতায় টেলর সিরিজ লিখুন ( এক্স-1) ফাংশন .

সমাধান.

সিরিজে একত্রিত হয় , অথবা -2< x£5।

কার্যকরী সিরিজের তত্ত্বে, কেন্দ্রীয় স্থানটি একটি ধারায় একটি ফাংশনের সম্প্রসারণের জন্য নিবেদিত বিভাগ দ্বারা দখল করা হয়।

সুতরাং, টাস্ক সেট করা হয়েছে: একটি প্রদত্ত ফাংশনের জন্য আমাদের এমন একটি পাওয়ার সিরিজ খুঁজে বের করতে হবে

যা একটি নির্দিষ্ট ব্যবধানে একত্রিত হয় এবং এর যোগফল ছিল সমান
, যারা

= ..

এই কাজ বলা হয় একটি পাওয়ার সিরিজে একটি ফাংশন প্রসারিত করার সমস্যা।

পাওয়ার সিরিজে একটি ফাংশনের পচনশীলতার জন্য একটি প্রয়োজনীয় শর্তএর পার্থক্য হল অসীম সংখ্যক বার - এটি কনভারজেন্ট পাওয়ার সিরিজের বৈশিষ্ট্যগুলি থেকে অনুসরণ করে। এই শর্তটি একটি নিয়ম হিসাবে, তাদের সংজ্ঞার ডোমেনে প্রাথমিক ফাংশনগুলির জন্য সন্তুষ্ট।

সুতরাং এর ফাংশন অনুমান করা যাক
যেকোন অর্ডারের ডেরিভেটিভ আছে। এটি একটি পাওয়ার সিরিজে প্রসারিত করা সম্ভব যদি তাই হয়, কিভাবে আমরা এই সিরিজ খুঁজে পেতে পারি? সমস্যার দ্বিতীয় অংশটি সমাধান করা সহজ, তাই এটি দিয়ে শুরু করা যাক।

ধরা যাক ফাংশনটি
বিন্দু সমন্বিত ব্যবধানে রূপান্তরিত একটি পাওয়ার সিরিজের যোগফল হিসাবে উপস্থাপন করা যেতে পারে এক্স 0 :

= .. (*)

যেখানে ক 0 ,এ 1 ,এ 2 ,...,এ n ,... - অজানা (এখনও) সহগ।

আসুন আমরা সমতা (*) মান রাখি x = x 0 , তারপর আমরা পেতে

.

আসুন আমরা পাওয়ার সিরিজ (*) টার্মকে টার্ম অনুসারে আলাদা করি

= ..

এবং এখানে বিশ্বাস x = x 0 , আমরা পাই

.

পরবর্তী পার্থক্যের সাথে আমরা সিরিজটি পাই

= ..

বিশ্বাসী x = x 0 , আমরা পাই
, কোথায়
.

পরে n- একাধিক পার্থক্য আমরা পেতে

শেষ সমতায় ধরে নিচ্ছি x = x 0 , আমরা পাই
, কোথায়

সুতরাং, সহগ পাওয়া যায়

,
,
, …,
,….,

সিরিজে যা প্রতিস্থাপন (*), আমরা পেতে

ফলে সিরিজ বলা হয় টেলরের পাশে ফাংশনের জন্য
.

এইভাবে, আমরা এটি প্রতিষ্ঠা করেছি যদি ফাংশনটিকে পাওয়ার সিরিজে পাওয়ার সিরিজে প্রসারিত করা যায় (x - x 0 ), তাহলে এই সম্প্রসারণটি অনন্য এবং ফলস্বরূপ সিরিজটি অগত্যা একটি টেলর সিরিজ।

উল্লেখ্য যে বিন্দুতে যেকোন অর্ডারের ডেরিভেটিভ আছে এমন যেকোন ফাংশনের জন্য টেলর সিরিজ পাওয়া যেতে পারে x = x 0 . তবে এর অর্থ এই নয় যে ফাংশন এবং ফলাফল সিরিজের মধ্যে একটি সমান চিহ্ন স্থাপন করা যেতে পারে, যেমন যে সিরিজের যোগফল মূল ফাংশনের সমান। প্রথমত, এই ধরনের সমতা শুধুমাত্র কনভারজেন্সের ক্ষেত্রেই বোঝা যায়, এবং ফাংশনের জন্য প্রাপ্ত টেলর সিরিজ ভিন্ন হতে পারে, এবং দ্বিতীয়ত, যদি টেলর সিরিজ একত্রিত হয়, তাহলে এর যোগফল মূল ফাংশনের সাথে মিলে নাও যেতে পারে।

3.2। একটি টেলর সিরিজের একটি ফাংশনের পচনশীলতার জন্য যথেষ্ট শর্ত

আসুন একটি বিবৃতি তৈরি করি যার সাহায্যে কাজটি সমাধান করা হবে।

যদি ফাংশন
বিন্দু x এর কিছু আশেপাশে 0 পর্যন্ত ডেরিভেটিভ আছে (n+ 1) এর অর্ডার অন্তর্ভুক্ত, তারপর এই আশেপাশে আমাদের আছেসূত্র টেলর

যেখানেআর n (এক্স)-টেলর সূত্রের অবশিষ্ট শব্দ - ফর্ম আছে (ল্যাগ্রেঞ্জ ফর্ম)

যেখানে বিন্দুξ x এবং x এর মধ্যে অবস্থিত 0 .

উল্লেখ্য যে টেলর সিরিজ এবং টেলর সূত্রের মধ্যে পার্থক্য রয়েছে: টেলর সূত্র একটি সসীম যোগফল, অর্থাৎ পি -নির্দিষ্ট সংখ্যা।

প্রত্যাহার যে সিরিজের যোগফল এস(x) আংশিক যোগফলের একটি কার্যকরী অনুক্রমের সীমা হিসাবে সংজ্ঞায়িত করা যেতে পারে এস n (x) কিছু ব্যবধানে এক্স:

.

এই অনুসারে, একটি ফাংশনকে একটি টেলর সিরিজে প্রসারিত করার অর্থ হল এমন একটি সিরিজ খুঁজে পাওয়া যা যেকোনো একটির জন্য এক্সএক্স

টেলরের সূত্র লিখি যেখানে ফর্মুলা

উল্লেখ্য যে
আমরা যে ত্রুটিটি পাই তা সংজ্ঞায়িত করে, ফাংশনটি প্রতিস্থাপন করি চ(x) বহুপদ এস n (x).

যদি
, যে
, যারা। ফাংশনটি একটি টেলর সিরিজে প্রসারিত হয়েছে। তদ্বিপরীত, যদি
, যে
.

এভাবে আমরা প্রমাণ করেছি একটি টেলর সিরিজের একটি ফাংশনের পচনশীলতার মানদণ্ড।

ফাংশন জন্য ক্রমচ(x) একটি টেলর সিরিজে প্রসারিত হয়, এই ব্যবধানে এটি প্রয়োজনীয় এবং যথেষ্ট
, কোথায়আর n (x) হল টেলর সিরিজের অবশিষ্ট শব্দ।

প্রণীত মানদণ্ড ব্যবহার করে, কেউ পেতে পারেন যথেষ্টএকটি টেলর সিরিজের একটি ফাংশনের পচনশীলতার শর্ত।

যদি ইনবিন্দু x এর কিছু পাড়া 0 ফাংশনের সমস্ত ডেরিভেটিভের পরম মান একই সংখ্যা M এর মধ্যে সীমাবদ্ধ≥ 0, অর্থাৎ

, টিo এই আশেপাশে ফাংশনটি একটি টেলর সিরিজে প্রসারিত হয়৷

উপরের থেকে এটি অনুসরণ করে অ্যালগরিদমফাংশন সম্প্রসারণ চ(x) টেলর সিরিজেএকটি বিন্দুর আশেপাশে এক্স 0 :

1. ফাংশনের ডেরিভেটিভস খোঁজা চ(x):

f(x), f’(x), f”(x), f’”(x), চ (n) (x),…

2. বিন্দুতে ফাংশনের মান এবং এর ডেরিভেটিভের মান গণনা করুন এক্স 0

f(x 0 ), f'(x 0 ), f”(x 0 ), f'"(x 0 ), চ (n) (x 0 ),…

3. আমরা আনুষ্ঠানিকভাবে টেলর সিরিজটি লিখি এবং ফলস্বরূপ পাওয়ার সিরিজের একত্রিত হওয়ার অঞ্চলটি খুঁজে পাই।

4. আমরা পর্যাপ্ত শর্ত পূরণের পরীক্ষা করি, যেমন যার জন্য আমরা প্রতিষ্ঠা করি এক্সঅভিসারী অঞ্চল থেকে, অবশিষ্ট শব্দ আর n (x) হিসাবে শূন্য ঝোঁক
বা
.

এই অ্যালগরিদম ব্যবহার করে একটি টেলর সিরিজে ফাংশন সম্প্রসারণ বলা হয় সংজ্ঞা অনুসারে একটি টেলর সিরিজে একটি ফাংশনের সম্প্রসারণবা সরাসরি পচন।