Хамгийн энгийн график хувиргалтууд. График хувиргах

Функцийн графикийг хөрвүүлэх

Энэ нийтлэлд би танд функцын графикуудын шугаман хувиргалтыг танилцуулж, эдгээр хувиргалтыг функцийн графикаас функцийн график гаргахад хэрхэн ашиглахыг танд үзүүлэх болно.

Функцийн шугаман хувиргалт нь функцийг өөрөө болон/эсвэл түүний аргументыг хэлбэрт шилжүүлэх явдал юм , түүнчлэн аргумент ба/эсвэл функцийн модулийг агуулсан хувиргалт.

Шугаман хувиргалтыг ашиглан график байгуулахад хамгийн их бэрхшээл үүсдэг дараагийн алхмууд:

1. Үндсэн функцийг тусгаарлах нь үнэндээ бидний хувиргаж буй график юм.
2. Өөрчлөлтийн дарааллын тодорхойлолтууд.

БАЭдгээр цэгүүд дээр бид илүү дэлгэрэнгүй ярих болно.

Функцийг нарийвчлан авч үзье

Энэ нь функц дээр суурилдаг. Түүнийг дуудъя үндсэн функц.

Функцийг зурахдаа Бид үндсэн функцийн график дээр хувиргалтыг хийдэг.

Хэрэв бид функцийн хувиргалтыг хийх байсан бол аргументийн тодорхой утгын хувьд түүний утгыг олсон дарааллаар, дараа нь

Аргумент, функцүүдийн шугаман хувиргалт ямар төрлүүд байдаг, тэдгээрийг хэрхэн гүйцэтгэх талаар авч үзье.

Аргументын хувиргалтууд.

1. f(x) f(x+b)

1. Функцийн графикийг байгуул

2. Функцийн графикийг OX тэнхлэгийн дагуу |b|-ээр шилжүүлнэ нэгж

• b>0 бол үлдсэн
• зөв бол b<0

Функцийн графикийг зурцгаая

1. Функцийн графикийг байгуул

2. Үүнийг 2 нэгж баруун тийш шилжүүлнэ үү:

2. f(x) f(kx)

1. Функцийн графикийг байгуул

2. Графикийн цэгүүдийн абсциссуудыг k-д хувааж, цэгүүдийн ординатыг өөрчлөхгүй.

Функцийн графикийг байгуулъя.

1. Функцийн графикийг байгуул

2. Графикийн цэгүүдийн бүх абсциссуудыг 2-т хувааж, ординатуудыг өөрчлөхгүй.

3. f(x) f(-x)

1. Функцийн графикийг байгуул

2. OY тэнхлэгтэй харьцуулахад тэгш хэмтэй байдлаар харуулах.

Функцийн графикийг байгуулъя.

1. Функцийн графикийг байгуул

2. OY тэнхлэгтэй харьцуулахад тэгш хэмтэй байдлаар харуулах:

4. f(x) f(|x|)

1. Функцийн графикийг байгуул

2. Графикийн OY тэнхлэгийн зүүн талд байрлах хэсгийг устгаж, OY тэнхлэгийн баруун талд байрлах графикийн хэсгийг OY тэнхлэгтэй харьцуулахад тэгш хэмтэйгээр гүйцээнэ.

Функцийн график дараах байдалтай байна.

Функцийн графикийг зурцгаая

1. Бид функцийн графикийг бүтээдэг (энэ нь OX тэнхлэгийн дагуу зүүн тийш 2 нэгжээр шилжсэн функцийн график юм):

2. OY (x) тэнхлэгийн зүүн талд байрлах графикийн хэсэг<0) стираем:

3. Графикийн OY тэнхлэгийн баруун талд байрлах хэсгийг (x>0) OY тэнхлэгтэй тэгш хэмтэйгээр гүйцээнэ.

Чухал! Аргументыг хувиргах хоёр үндсэн дүрэм.

1. Бүх аргументын хувиргалтыг OX тэнхлэгийн дагуу гүйцэтгэнэ

2. Аргументийн бүх хувиргалтыг “эсрэгээр”, “урвуу дарааллаар” гүйцэтгэдэг.

Жишээлбэл, функцэд аргументыг хувиргах дараалал дараах байдалтай байна.

1. х-ийн модулийг ав.

2. X модульд 2-ын тоог нэмнэ.

Гэхдээ бид графикийг урвуу дарааллаар бүтээв:

Эхлээд 2-р хувиргалтыг хийсэн - графикийг зүүн тийш 2 нэгжээр шилжүүлсэн (өөрөөр хэлбэл цэгүүдийн абсциссыг "урвуу" байдлаар 2-оор багасгасан)

Дараа нь f(x) f(|x|) хувиргалтыг хийлээ.

Товчхондоо хувиргалтын дарааллыг дараах байдлаар бичнэ.

Одоо ярилцъя функцын хувиргалт . Өөрчлөлтүүд явагдаж байна

1. OY тэнхлэгийн дагуу.

2. Үйлдлийг гүйцэтгэх дарааллаар.

Эдгээр өөрчлөлтүүд нь:

1. f(x)f(x)+D

2. OY тэнхлэгийн дагуу |D|-ээр шилжүүлнэ нэгж

• D>0 бол дээш
• доошоо бол D<0

Функцийн графикийг зурцгаая

1. Функцийн графикийг байгуул

2. Үүнийг OY тэнхлэгийн дагуу 2 нэгж дээш шилжүүлнэ:

2. f(x)Af(x)

1. y=f(x) функцийн графикийг байгуул.

2. Графикийн бүх цэгийн ординатуудыг А-аар үржүүлж, абсциссуудыг өөрчлөхгүй.

Функцийн графикийг зурцгаая

1. Функцийн графикийг байгуулъя

2. График дээрх бүх цэгийн ординатыг 2-оор үржүүл.

3.f(x)-f(x)

1. y=f(x) функцийн графикийг байгуул.

Функцийн графикийг байгуулъя.

1. Функцийн графикийг байгуул.

2. Бид үүнийг OX тэнхлэгтэй харьцуулахад тэгш хэмтэй байдлаар харуулдаг.

4. f(x)|f(x)|

1. y=f(x) функцийн графикийг байгуул.

2. Графикийн OX тэнхлэгээс дээш байрлах хэсгийг өөрчлөхгүй, OX тэнхлэгийн доор байрлах графикийн хэсгийг энэ тэнхлэгтэй харьцуулахад тэгш хэмтэй харуулна.

Функцийн графикийг зурцгаая

1. Функцийн графикийг байгуул. Үүнийг OY тэнхлэгийн дагуу функцын графикийг 2 нэгжээр доош шилжүүлэх замаар олж авна.

2. Одоо бид графикийн OX тэнхлэгийн доор байрлах хэсгийг энэ тэнхлэгтэй харьцуулахад тэгш хэмтэй байдлаар харуулах болно.

Эцсийн хувиргалтыг хатуу хэлэхэд функцын хувиргалт гэж нэрлэх боломжгүй, учир нь энэхүү хувиргалтын үр дүн нь функц байхаа больсон.

|y|=f(x)

1. y=f(x) функцийн графикийг байгуул.

2. Бид графикийн OX тэнхлэгийн доор байрлах хэсгийг устгаж, дараа нь энэ тэнхлэгтэй харьцуулахад OX тэнхлэгээс дээш байрлах графикийн хэсгийг тэгш хэмтэйгээр гүйцээнэ.

Тэгшитгэлийг зуръя

1. Бид функцийн графикийг байгуулна:

2. Графикийн OX тэнхлэгийн доор байрлах хэсгийг арилга.

3. Бид энэ тэнхлэгтэй харьцуулахад OX тэнхлэгээс дээш байрлах графикийн хэсгийг тэгш хэмтэйгээр гүйцээнэ.

Эцэст нь би функцийн график байгуулах алхам алхмаар алгоритмыг харуулсан ВИДЕО СУРГАЛТ үзэхийг санал болгож байна.

Энэ функцийн график дараах байдалтай байна.

Буцах Урагшаа

Анхаар! Слайдыг урьдчилан үзэх нь зөвхөн мэдээллийн зорилгоор хийгдсэн бөгөөд үзүүлэнгийн бүх шинж чанарыг илэрхийлэхгүй байж болно. Хэрэв та сонирхож байвал энэ ажил, бүрэн хувилбарыг нь татаж авна уу.

Хичээлийн зорилго:Функцийн графикийг хувиргах зүй тогтлыг тодорхойлох.

Даалгаварууд:

Боловсролын:

• Оюутнуудад өгөгдсөн функцийн графикийг хувиргах, параллель орчуулга, шахалт (суналт) ашиглан функцийн график байгуулахыг заах. янз бүрийн төрөлтэгш хэм.

Боловсролын:

• Хүмүүжүүл хувийн чанаруудоюутнууд (сонсох чадвар), бусдад сайн сайхан сэтгэл, анхаарал болгоомжтой байх, үнэн зөв, сахилга бат, бүлэгт ажиллах чадвар.
• Сэдвийн сонирхол, мэдлэг олж авах хэрэгцээг төлөвшүүлэх.

Хөгжлийн:

• Оюутнуудын орон зайн төсөөлөл, логик сэтгэлгээг хөгжүүлэх, хүрээлэн буй орчныг хурдан жолоодох чадварыг хөгжүүлэх; оюун ухаан, авхаалж самбаа, ой санамжийг хөгжүүлэх.

Тоног төхөөрөмж:

• Мультимедиа суурилуулалт: компьютер, проектор.

Уран зохиол:

1. Башмаков, M.I. Математик [Текст]: Эхлэх байгууллагуудад зориулсан сурах бичиг. болон Лхагва гараг проф. боловсрол / M.I. Башмаков - 5-р хэвлэл, шинэчилсэн. – М.: “Академи” хэвлэлийн төв, 2012. – 256 х.
2. Башмаков, M.I. Математик. Асуудлын ном [Текст]: сурах бичиг.

боловсролын тэтгэмж байгууллагууд эрт болон Лхагва гараг

1. проф. боловсрол / M. I. Башмаков. – М.: “Академи” хэвлэлийн төв, 2012. – 416 х.
2. Хичээлийн төлөвлөгөө:
3. Зохион байгуулалтын мөч (3 мин).
4. Мэдлэгийг шинэчлэх (7 мин).
5. Шинэ материалын тайлбар (20 мин).
6. Шинэ материалыг нэгтгэх (10 мин).Хичээлийн хураангуй (3 мин).

Гэрийн даалгавар

(2 мин).

Хичээлийн явц

1. Org. мөч (3 мин).

Байгаа хүмүүсийг шалгаж байна.

Хичээлийн зорилгыг илэрхийлэх.

Хувьсах хэмжигдэхүүнүүдийн хоорондын хамаарал болох функцүүдийн үндсэн шинж чанарууд нь эдгээр хэмжигдэхүүнүүдийг хэмжих аргыг өөрчлөх үед, өөрөөр хэлбэл хэмжилтийн хуваарь ба лавлах цэгийг өөрчлөх үед мэдэгдэхүйц өөрчлөгдөх ёсгүй. Гэсэн хэдий ч хувьсах хэмжигдэхүүнийг хэмжих аргыг илүү оновчтой сонгосон тул тэдгээрийн хоорондын хамаарлын бичлэгийг хялбаршуулж, энэ бичлэгийг зарим стандарт хэлбэрт оруулах боломжтой байдаг. Геометрийн хэлээр хэмжигдэхүүнийг хэмжих аргыг өөрчлөх нь графикуудын зарим энгийн хувиргалтыг хэлнэ гэсэн үг бөгөөд бид өнөөдөр үүнийг судлах болно.

2. Мэдлэгээ шинэчлэх (7 мин).

График хувиргалтын талаар ярихаасаа өмнө авч үзсэн материалаа тоймлон үзье.

Аман ажил. (Слайд 2). , , , .

Өгөгдсөн функцууд:

3. Функцийн графикуудыг тайлбарла. 3. Шинэ материалын тайлбар (20 мин).Графикуудын хамгийн энгийн хувиргалт нь тэдгээрийн зэрэгцээ шилжүүлэлт, шахалт (суналт) болон зарим төрлийн тэгш хэм юм. Зарим өөрчлөлтийг хүснэгтэд үзүүлэв

(Хавсралт 1)

, (Слайд 3).

Бүлгээр ажиллах.	Бүлэг бүр өгөгдсөн функцүүдийн графикийг байгуулж, үр дүнг хэлэлцүүлэгт танилцуулна.	Чиг үүрэг	Функцийн графикийг хувиргах
	Функцийн жишээдээр Анэгж хүртэл бол А>0 ба |A| дээр нэгж буурсан бол А<0.	,	(Слайд 4)
	Тэнхлэгийн дагуу параллель дамжуулалт Өөдээр Анэгж бол баруун тийш А>0 ба асаалттай - Азүүн талд нэгж бол А<0.	,	(Слайд 5)

Өөрчлөлтгүй цэвэр хэлбэрээр үндсэн үндсэн функцүүд ховор байдаг тул ихэнхдээ та тогтмол болон коэффициент нэмэх замаар үндсэн функцүүдээс олж авсан үндсэн функцүүдтэй ажиллах хэрэгтэй болдог. Ийм графикийг өгөгдсөн геометрийн хувиргалтыг ашиглан бүтээдэг үндсэн функцууд.

y = - 1 3 x + 2 3 2 + 2 хэлбэрийн квадрат функцийн жишээг авч үзье, график нь y = x 2 парабол болох бөгөөд энэ нь Oy-ийн хувьд гурван удаа шахагдсан ба тэгш хэмтэй байна. Үхэр рүү, мөн Үхрийн дагуу баруун тийш 2 3-аар шилжиж, Ой дагуу 2 нэгжээр дээшилсэн. Координатын шугам дээр дараах байдалтай харагдана.

Yandex.RTB R-A-339285-1

Функцийн графикийн геометрийн хувиргалт

Өгөгдсөн графикийн геометрийн хувиргалтыг ашигласнаар бид графикийг k 1 > 0, k 2 > 0 үед ± k 1 · f (± k 2 · (x + a)) + b хэлбэрийн функцээр дүрсэлсэн болохыг олж мэдэв. шахалтын коэффициентүүд нь 0 байна< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >O y ба O x-ийн дагуу 1, k 2 > 1. k 1 ба k 2 коэффициентүүдийн урд талын тэмдэг нь тэнхлэгүүдтэй харьцуулахад графикийн тэгш хэмтэй дэлгэцийг харуулж, a ба b нь O x ба O y дагуу шилжинэ.

Тодорхойлолт 1

3 төрөл байдаг графикийн геометрийн хувиргалт:

• Томруулах O x ба O y дагуу. Үүнд k 1 ба k 2 коэффициентүүд 0 байхад 1-тэй тэнцүү биш байвал нөлөөлнө< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, дараа нь графикийг O y дагуу сунгаж, O x дагуу шахна.
• Координатын тэнхлэгтэй харьцуулахад тэгш хэмтэй дэлгэц.Хэрэв k 1-ийн өмнө “-” тэмдэг байвал тэгш хэм нь O x-тэй, k 2-ын өмнө O y-тэй харьцангуй байна. Хэрэв "-" байхгүй бол асуудлыг шийдвэрлэхдээ алгасах болно;
• Зэрэгцээ дамжуулалт (ээлж) O x ба O y дагуу. 0-тэй тэнцүү биш a ба b коэффициентүүд байвал хувиргалтыг хийнэ. Хэрэв а эерэг байвал графикийг зүүн тийш |-ээр шилжүүлнэ a | нэгж, хэрэв a сөрөг байвал ижил зайд баруун тийш. b утга нь O y тэнхлэгийн дагуух хөдөлгөөнийг тодорхойлдог бөгөөд энэ нь b эерэг үед функц дээш, b сөрөг үед доош шилжинэ гэсэн үг юм.

-ээс эхлээд жишээнүүдийг ашиглан шийдлүүдийг авч үзье эрчим хүчний функц.

Жишээ 1

y = x 2 3-ийг хувиргаж, y = - 1 2 · 8 x - 4 2 3 + 3 функцийн графикийг зур.

Шийдэл

Функцуудыг дараах байдлаар илэрхийлье.

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

k 1 = 2 тохиолдолд "-", a = - 1 2, b = 3 байгаа эсэхийг анхаарч үзэх нь зүйтэй. Эндээс бид геометрийн хувиргалтыг O y-ийн дагуу хоёр удаа сунгаж, O x-тэй харьцуулахад тэгш хэмтэй байдлаар харуулж, баруун тийш 1 2, дээш 3 нэгжээр шилжсэн болохыг олж мэднэ.

Хэрэв бид анхны чадлын функцийг дүрсэлсэн бол бид үүнийг олж авна

O y дагуу хоёр удаа сунгасан үед бид тэр байна

O x-тэй тэгш хэмтэй зураглал нь хэлбэртэй байна

ба баруун тийш 1 2-оор шилжинэ

дээш 3 нэгжийн хөдөлгөөн шиг харагдаж байна

Экспоненциал функцүүдийн хувиргалтыг жишээн дээр авч үзье.

Жишээ 2

y = - 1 2 1 2 (2 - x) + 8 экспоненциал функцийн графикийг байгуул.

Шийдэл.

Хүчин чадлын функцийн шинж чанарт үндэслэн функцийг хувиргая. Дараа нь бид үүнийг авдаг

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Эндээс бид y = 1 2 x хувиргалтын гинжин хэлхээг олж авна.

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Бид эхийг нь олж мэднэ экспоненциал функцшиг харагдаж байна

O y дагуу хагасыг нь шахаж өгдөг

O x дагуу сунах

O x-тэй холбоотой тэгш хэмтэй зураглал

Зураглал нь O y-тэй харьцуулахад тэгш хэмтэй байна

8 нэгж дээш хөдөл

Жишээ ашиглан шийдлийг харцгаая логарифм функц y = log(x) .

Жишээ 3

y = ln (x) хувиргалтыг ашиглан y = ln e 2 · - 1 2 x 3 функцийг байгуул.

Шийдэл

Үүнийг шийдэхийн тулд логарифмын шинж чанарыг ашиглах шаардлагатай бол бид дараахь зүйлийг авна.

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Логарифм функцийн хувиргалт дараах байдалтай байна.

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Анхны логарифм функцийг зуръя

Бид системийг O y-ийн дагуу шахдаг

Бид O x-ийн дагуу сунадаг

Бид O y-тэй холбоотой зураглалыг хийдэг

Бид 2 нэгжээр шилжиж, бид авдаг

Графикуудыг хөрвүүлэхийн тулд тригонометрийн функц± k 1 · f (± k 2 · (x + a)) + b хэлбэрийн шийдлийн схемийг тохируулах шаардлагатай. k 2 нь T k 2-тэй тэнцүү байх шаардлагатай. Эндээс бид 0-ийг авна< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

y = sin x хувиргалттай бодлого бодох жишээг авч үзье.

Жишээ 4

y=sinx функцийн хувиргалтыг ашиглан y = - 3 sin 1 2 x - 3 2 - 2-ын графикийг байгуул.

Шийдэл

Функцийг ± k 1 · f ± k 2 · x + a + b хэлбэрт оруулах шаардлагатай. Үүнийг хийхийн тулд:

y = - 3 нүгэл 1 2 x - 3 2 - 2 = - 3 нүгэл 1 2 (x - 3) - 2

Эндээс k 1 = 3, k 2 = 1 2, a = - 3, b = - 2 байгааг харж болно. k 1-ийн өмнө "-" байгаа боловч k 2-оос өмнө биш тул бид хэлбэрийн хувиргалтын гинжийг авна.

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 син 1 2 (x - 3) - 2

Нарийвчилсан синус долгионы хувиргалт. Анхны синусоид y = sin (x) графикийг зурахдаа бид хамгийн бага эерэг үеийг T = 2 π гэж үздэг болохыг олж мэдэв. π 2 + 2 π · k цэгүүдэд хамгийн ихийг олох; 1, хамгийн бага нь - - π 2 + 2 π · k; - 1, k ∈ Z.

O y нь 3 дахин сунадаг бөгөөд энэ нь хэлбэлзлийн далайцын өсөлт 3 дахин нэмэгдэнэ гэсэн үг юм. T = 2 π нь хамгийн бага эерэг үе юм. Хамгийн их хэмжээ нь π 2 + 2 π · k руу очно; 3, k ∈ Z, минимум - - π 2 + 2 π · k; - 3, k ∈ Z.

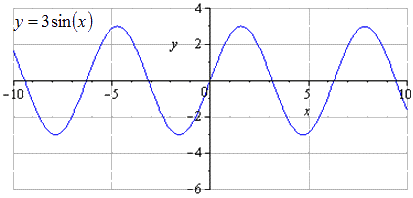
O x-ийн дагуу хагасаар сунгах үед бид хамгийн бага эерэг үе нь 2 дахин нэмэгдэж, T = 2 π k 2 = 4 π-тэй тэнцүү болохыг олж мэдэв. Хамгийн дээд хэмжээ нь π + 4 π · k хүртэл явагдана; 3, k ∈ Z, минимумууд – in - π + 4 π · k; - 3, k ∈ Z.

Зураг нь O x-тэй харьцуулахад тэгш хэмтэй байна. Энэ тохиолдолд хамгийн бага эерэг үе өөрчлөгдөхгүй бөгөөд T = 2 π k 2 = 4 π-тэй тэнцүү байна. Хамгийн их шилжилт нь - π + 4 π · k; 3, k ∈ Z, хамгийн бага нь π + 4 π · k; - 3, k ∈ Z.

График 2 нэгжээр доош шилжсэн. Хамгийн бага нийтлэг хугацаанд өөрчлөлт ороогүй болно. Цэг рүү шилжих максимумыг олох - π + 3 + 4 π · k; 1, k ∈ Z, хамгийн бага - π + 3 + 4 π · k; - 5 , k ∈ Z .

Энэ үе шатанд тригонометрийн функцийн графикийг хувиргасан гэж үзнэ.

y = cos x функцийн нарийвчилсан хувиргалтыг авч үзье.

Жишээ 5

y = cos x хэлбэрийн функцийн хувиргалтыг ашиглан y = 3 2 cos 2 - 2 x + 1 функцийн графикийг байгуул.

Шийдэл

Алгоритмын дагуу өгөгдсөн функцийг ± k 1 · f ± k 2 · x + a + b хэлбэрт оруулах шаардлагатай. Дараа нь бид үүнийг авдаг

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Нөхцөлөөс харахад k 1 = 3 2, k 2 = 2, a = - 1, b = 1, k 2 нь “-” байх боловч k 1-ээс өмнө байхгүй байна.

Эндээс бид дараах хэлбэрийн тригонометрийн функцийн графикийг олж авлаа.

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

График дүрс бүхий косинусыг алхам алхмаар хувиргах.

y = cos (x) графикийг өгвөл хамгийн бага нь тодорхой байна ерөнхий үетэнцүү T = 2 π. 2 π · k -д максимум олох; 1, k ∈ Z ба π + 2 π · k минимум байна; - 1, k ∈ Z.

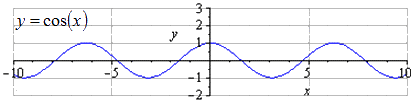
Ойн дагуу 3 2 дахин сунгахад хэлбэлзлийн далайц 3 2 дахин нэмэгддэг. T = 2 π нь хамгийн бага эерэг үе юм. 2 π · k -д максимум олох; 3 2, k ∈ Z, π + 2 π · k дахь минимум; - 3 2 , k ∈ Z .

O x-ийн дагуу хагасаар шахагдсан үед бид хамгийн бага эерэг үе нь T = 2 π k 2 = π тоо болохыг олж мэднэ. Максимуудын π · k руу шилжих шилжилт явагдана; 3 2, k ∈ Z, хамгийн бага - π 2 + π · k; - 3 2 , k ∈ Z .

Ойтой холбоотой тэгш хэмтэй зураглал. График нь сондгой тул өөрчлөгдөхгүй.

График 1-ээр шилжих үед. Хамгийн бага эерэг үед өөрчлөлт байхгүй T = π. π · k + 1-д максимум олох; 3 2, k ∈ Z, хамгийн бага - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

1-ээр шилжихэд хамгийн бага эерэг үе нь T = π-тэй тэнцүү бөгөөд өөрчлөгдөхгүй. π · k + 1-д максимум олох; 5 2, k ∈ Z, π 2 + 1 + π · k дахь минимум; - 1 2 , k ∈ Z .

Косинусын функцийн хувиргалт дууссан.

y = t g x жишээн дээр хувиргалтыг авч үзье.

Жишээ 6

y = t g (x) функцийн хувиргалтыг ашиглан y = - 1 2 t g π 3 - 2 3 x + π 3 функцийн графикийг байгуул.

Шийдэл

Эхлэхийн тулд өгөгдсөн функцийг ± k 1 · f ± k 2 · x + a + b хэлбэрт оруулах шаардлагатай бөгөөд үүний дараа бид үүнийг олж авна.

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, k 1 ба k 2 илтгэлцүүрүүдийн урд “-” байгаа нь тодорхой харагдаж байна. Энэ нь тангенсоидуудыг хувиргасны дараа бид авдаг гэсэн үг юм

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

График дүрслэл бүхий шүргэгчийг алхам алхмаар хувиргах.

Бидэнд анхны график нь y = t g (x) байна. Эерэг хугацааны өөрчлөлт нь T = π-тэй тэнцүү байна. Тодорхойлолтын домэйн гэж үздэг - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Бид үүнийг Oy дагуу 2 удаа шахдаг. T = π нь хамгийн бага эерэг үе гэж тооцогддог бөгөөд тодорхойлолтын хүрээ нь - π 2 + π · k хэлбэртэй байна; π 2 + π · k, k ∈ Z.

O x 3-ын дагуу 2 удаа сунгана. Хамгийн бага эерэг үеийг тооцоолъё, энэ нь T = π k 2 = 3 2 π -тэй тэнцүү байсан. Мөн координат бүхий функцийг тодорхойлох муж нь 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, зөвхөн тодорхойлолтын муж өөрчлөгдөнө.

Тэгш хэм нь O x тал дээр явагддаг. Энэ хугацаанд хугацаа өөрчлөгдөхгүй.

Координатын тэнхлэгүүдийг тэгш хэмтэйгээр харуулах шаардлагатай. Энэ тохиолдолд тодорхойлолтын домэйн өөрчлөгдөөгүй байна. Хуваарь нь өмнөхтэй нь таарч байна. Энэ нь шүргэгч функц нь сондгой байгааг харуулж байна. Хэрэв тэгвэл сондгой функц O x ба O y-ийн тэгш хэмтэй зураглалыг тохируулж, дараа нь анхны функц руу шилжүүлнэ.

Физик үйл явцын нөхцлөөс хамааран зарим хэмжигдэхүүн нь тогтмол утгыг авч, тогтмол гэж нэрлэдэг, зарим нь тодорхой нөхцөлд өөрчлөгдөж, хувьсагч гэж нэрлэгддэг.

Анхааралтай судлах орчингэдгийг харуулж байна физик хэмжигдэхүүнүүдбие биенээсээ хамааралтай, өөрөөр хэлбэл зарим хэмжигдэхүүн өөрчлөгдөх нь бусад нь өөрчлөгдөхөд хүргэдэг.

Математик шинжилгээ нь бие биенээсээ тодорхой утгыг хийсвэрлэн өөр өөр хэмжигдэхүүнүүдийн тоон хамаарлыг судалдаг. Математик шинжилгээний үндсэн ойлголтуудын нэг бол функцийн тухай ойлголт юм.

Олонлогийн элементүүд болон олонлогийн элементүүдийг авч үзье
(Зураг 3.1).

Хэрэв олонлогийн элементүүдийн хооронд зарим захидал харилцаа тогтоогдвол
Тэгээд дүрэм хэлбэрээр , дараа нь тэд функц тодорхойлогдсон болохыг тэмдэглэв
.

Тодорхойлолт 3.1. Захидал , элемент бүртэй холбоотой хоосон багц биш
зарим нэг сайн тодорхойлсон элемент хоосон багц биш ,функц эсвэл зураглал гэж нэрлэдэг
В .

Бэлгэдлийн хэлбэрээр харуулах
В дараах байдлаар бичигдсэн байна.

.

Үүний зэрэгцээ олон
функцийн тодорхойлолтын муж гэж нэрлэгдэх ба тэмдэглэнэ
.

Эргээд олон функцийн утгын муж гэж нэрлэгдэх ба тэмдэглэнэ
.

Үүнээс гадна багцын элементүүдийг тэмдэглэх нь зүйтэй
бие даасан хувьсагч, олонлогийн элементүүд гэж нэрлэдэг хамааралтай хувьсагч гэж нэрлэдэг.

Функцийг тодорхойлох аргууд

Функцийг дараах үндсэн аргаар тодорхойлж болно: хүснэгт, график, аналитик.

Хэрэв туршилтын өгөгдөл дээр үндэслэн функцийн утгууд болон холбогдох аргументуудын утгыг агуулсан хүснэгтүүдийг эмхэтгэсэн бол функцийг тодорхойлох энэ аргыг хүснэгт гэж нэрлэдэг.

Үүний зэрэгцээ, туршилтын үр дүнгийн зарим судалгааг бичигч (осциллограф, бичигч гэх мэт) дээр харуулсан бол функцийг графикаар зааж өгсөн болохыг тэмдэглэнэ.

Хамгийн түгээмэл нь функцийг тодорхойлох аналитик арга юм, i.e. бие даасан болон хамааралтай хувьсагчийг томьёо ашиглан холбох арга. Энэ тохиолдолд функцийг тодорхойлох домэйн чухал үүрэг гүйцэтгэдэг.

ялгаатай боловч тэдгээр нь ижил аналитик харилцаагаар өгөгддөг.

Хэрэв та зөвхөн функцийн томъёог зааж өгвөл
, дараа нь энэ функцийн тодорхойлолтын домэйн нь хувьсагчийн эдгээр утгуудын олонлогтой давхцаж байна гэж бид үзэж байна. , үүний төлөө илэрхийлэл
утга учиртай. Үүнтэй холбогдуулан функцийн тодорхойлолтын мужийг олох асуудал онцгой үүрэг гүйцэтгэдэг.

Даалгавар 3.1. Функцийн домайныг ол

Шийдэл

Эхний нэр томъёо нь хэзээ бодит утгыг авдаг
, хоёр дахь нь цагт. Тиймээс өгөгдсөн функцийн тодорхойлолтын мужийг олохын тулд тэгш бус байдлын системийг шийдэх шаардлагатай.

Үүний үр дүнд ийм тогтолцооны шийдэл нь . Тиймээс функцийн тодорхойлолтын муж нь сегмент юм
.

Функцийн графикуудын хамгийн энгийн хувиргалтууд

Хэрэв та үндсэн үндсэн функцүүдийн сайн мэддэг графикийг ашиглавал функцийн графикийг бүтээх ажлыг ихээхэн хялбарчилж болно. Дараах функцуудыг үндсэн үндсэн функцууд гэж нэрлэдэг.

1) эрчим хүчний функц
Хаана
;

2) экспоненциал функц
Хаана
Тэгээд
;

3) логарифм функц
, Хаана - нэгээс бусад эерэг тоо:
Тэгээд
;

4) тригонометрийн функцууд




;
.

5) урвуу тригонометрийн функцууд
;
;
;
.

Дөрвөн арифметик үйлдлүүд болон хязгаарлагдмал тооны давхцалуудыг ашиглан үндсэн үндсэн функцуудаас олж авсан функцуудыг энгийн функцууд гэнэ.

Энгийн геометрийн хувиргалт нь функцүүдийн графикийг бүтээх үйл явцыг хялбаршуулах боломжийг олгодог. Эдгээр өөрчлөлтүүд нь дараах мэдэгдлүүд дээр суурилдаг.

y=f(x+a) функцийн график нь y=f(x), шилжсэн график (a >0 зүүн тийш, a хувьд)< 0 вправо) на |a| единиц параллельно осиOx.

y=f(x) +b функцийн график нь y=f(x), шилжсэн (b>0-д дээш, b үед) график юм.< 0 вниз) на |b| единиц параллельно осиOy.

y = mf(x) (m0) функцийн график нь y = f(x) сунасан (m>1 үед) m удаа эсвэл шахсан (0 үед) график юм.

y = f(kx) функцийн график нь y = f(x), шахагдсан (k >1 хувьд) k удаа эсвэл сунгасан (0 хувьд) график юм.< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.