Функцуудыг чадлын цуврал болгон өргөжүүлэх. Фурье цуврал. Функцийг Фурье цуврал болгон өргөжүүлэх. Функцийг синусын болон косинусуудын цуврал болгон өргөтгөх

2π үетэй үечилсэн функцийн Фурье цуврал.

Фурье цуврал нь үечилсэн функцийг бүрэлдэхүүн хэсгүүдэд задлах замаар судлах боломжийг бидэнд олгодог. Хувьсах гүйдэл ба хүчдэл, шилжилт хөдөлгөөн, бүлүүрт механизмын хурд ба хурдатгал ба акустик долгион нь инженерийн тооцоололд үечилсэн функцийг ашиглах ердийн практик жишээ юм.

Фурье цувралын өргөтгөл нь -π ≤x≤ π интервал дахь практик ач холбогдолтой бүх функцийг нийлсэн тригонометрийн цуваа хэлбэрээр илэрхийлж болно гэсэн таамаглал дээр суурилдаг (хэрэв хэсэгчилсэн нийлбэрүүдийн дараалал нь түүний нөхцлөөс бүрдсэн бол цувралыг нийлсэн гэж үзнэ. нийлдэг):

Sinx болон cosx-ийн нийлбэрээр дамжуулан стандарт (=ердийн) тэмдэглэгээ

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

Энд a o, a 1,a 2,...,b 1,b 2,.. нь бодит тогтмолууд, өөрөөр хэлбэл.

-π-аас π хүртэлх мужид Фурье цувралын коэффициентийг дараах томъёогоор тооцоолно.

a o , a n ба b n коэффициентүүдийг нэрлэнэ Фурье коэффициентүүд, хэрэв тэдгээрийг олох боломжтой бол (1) цувралыг дуудна Фурьегийн ойролцоо, f(x) функцтэй харгалзах. Цуврал (1)-ийн хувьд (a 1 cosx+b 1 sinx) нэр томъёог эхний буюу гэж нэрлэдэг үндсэн гармоник,

Цуврал бичих өөр нэг арга бол acosx+bsinx=csin(x+α) хамаарлыг ашиглах явдал юм.

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Энд a o нь тогтмол бөгөөд 1 =(a 1 2 +b 1 2) 1/2, n =(a n 2 +b n 2) 1/2 - янз бүрийн бүрэлдэхүүн хэсгүүдийн далайц ба n =arctg-тэй тэнцүү байна. a n /b n.

(1) цувралын хувьд (a 1 cosx+b 1 sinx) эсвэл c 1 sin(x+α 1) нэр томъёог эхний буюу үндсэн гармоник,(a 2 cos2x+b 2 sin2x) эсвэл c 2 sin(2x+α 2)-ийг гэнэ. хоёр дахь гармоникгэх мэт.

Нарийн төвөгтэй дохиог үнэн зөв илэрхийлэхийн тулд хязгааргүй тооны нэр томъёо шаардагдана. Гэсэн хэдий ч олон практик асуудалд зөвхөн эхний хэдэн нэр томъёог авч үзэх нь хангалттай юм.

2π үетэй үечилсэн бус функцүүдийн Фурье цуваа.

Тогтмол бус функцийг өргөжүүлэх.

Хэрэв f(x) функц нь үечилсэн биш бол энэ нь x-ийн бүх утгын хувьд Фурье цуврал болгон өргөжүүлэх боломжгүй гэсэн үг юм. Гэсэн хэдий ч 2π өргөнтэй аль ч муж дахь функцийг илэрхийлэх Фурье цувралыг тодорхойлох боломжтой.

Тогтмол бус функцийн хувьд тодорхой муж доторх f(x) утгуудыг сонгож, 2π интервалаар тухайн мужаас гадуур давтах замаар шинэ функцийг байгуулж болно. Шинэ функц нь 2π үетэй үе үе байдаг тул x-ийн бүх утгын хувьд үүнийг Фурье цуврал болгон өргөжүүлж болно. Жишээлбэл, f(x)=x функц нь үечилсэн биш юм. Гэсэн хэдий ч хэрэв үүнийг o-оос 2π хүртэлх зайд Фурьегийн цуваа болгон өргөжүүлэх шаардлагатай бол энэ интервалаас гадуур 2π үетэй үечилсэн функцийг байгуулна (доорх зурагт үзүүлэв).

f(x)=x гэх мэт үечилсэн бус функцүүдийн хувьд Фурье цувааны нийлбэр нь тухайн муж дахь бүх цэг дэх f(x)-ийн утгатай тэнцүү боловч цэгүүдийн хувьд f(x)-тай тэнцүү биш байна. хүрээнээс гадуур. 2π муж дахь үечилсэн бус функцийн Фурье цувралыг олохын тулд Фурье коэффициентийн ижил томъёог ашиглана.

Тэгш ба сондгой функцууд.

Тэд y=f(x) функцийг хэлдэг. бүр, хэрэв x-ийн бүх утгын хувьд f(-x)=f(x) бол. Тэгш функцүүдийн графикууд нь y тэнхлэгтэй харьцуулахад үргэлж тэгш хэмтэй байдаг (өөрөөр хэлбэл тэдгээр нь толин тусгал дүрс юм). Тэгш функцүүдийн хоёр жишээ: y=x2 ба y=cosx.

Тэд y=f(x) функц гэж хэлдэг. хачин,Хэрэв x-ийн бүх утгын хувьд f(-x)=-f(x) байвал. Хачирхалтай функцүүдийн графикууд нь гарал үүслийн хувьд үргэлж тэгш хэмтэй байдаг.

Олон функц тэгш, сондгой ч биш.

Косинус дахь Фурье цувралын өргөтгөл.

2π үетэй тэгш үечилсэн функцийн Фурье цуврал f(x) нь зөвхөн косинусын гишүүн (жишээ нь, синусын гишүүн байхгүй) бөгөөд тогтмол гишүүнийг агуулж болно. Тиймээс,

Фурье цувралын коэффициентүүд хаана байна,

2π үетэй f(x) сондгой үечилсэн функцийн Фурье цуваа нь зөвхөн синустай гишүүдийг агуулна (өөрөөр хэлбэл косинустай гишүүдийг агуулаагүй).

Тиймээс,

Фурье цувралын коэффициентүүд хаана байна,

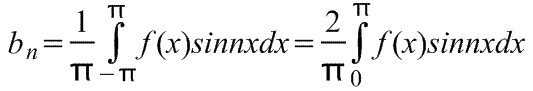
Хагас мөчлөгийн Фурье цуврал.

Хэрэв функц нь зөвхөн 0-ээс 2π хүртэл биш 0-ээс π хүртэлх мужид тодорхойлогдсон бол түүнийг зөвхөн синус эсвэл зөвхөн косинусын цуваагаар өргөжүүлж болно. Үр дүнд нь Фурье цуврал гэж нэрлэдэг Хагас мөчлөгийн үед Фурьегийн ойролцоо.

Хэрэв та задралыг авахыг хүсвэл Хагас мөчлөгийн Фурье косинусаар f(x) функцууд 0-ээс π хүртэлх зайд байвал тэгш үечилсэн функц байгуулах шаардлагатай. Зураг дээр. x=0-ээс x=π хүртэлх интервал дээр бүтээгдсэн f(x)=x функцийг доор харуулав. Түүнээс хойш жигд функц f(x) тэнхлэгт тэгш хэмтэй, AB шугамыг зурж үзүүлсний дагуу зур. доор. Хэрэв бид авч үзсэн интервалаас гадуур үүссэн гурвалжин хэлбэр нь 2π үетэй үе үе байна гэж үзвэл эцсийн график дараах байдалтай байна. Зураг дээр. доор. Бид өмнөх шигээ Фурье тэлэлтийг косинусаар олж авах шаардлагатай байгаа тул Фурье коэффициент a o ба a n-ийг тооцоолно.

Хэрэв та авах шаардлагатай бол Фурье хагас циклийн синусын тэлэлт f(x) функц нь 0-ээс π хүртэлх зайд байгаа бол сондгой үечилсэн функц байгуулах шаардлагатай. Зураг дээр. x=0-ээс x=π хүртэлх интервал дээр бүтээгдсэн f(x)=x функцийг доор харуулав. Сондгой функц нь гарал үүслийн хувьд тэгш хэмтэй байдаг тул бид CD шугамыг зурж үзүүлсний дагуу байгуулна. Хэрэв бид авч үзсэн интервалаас гадуур үүссэн хөрөөний дохио нь 2π-ийн үетэй үе үе байна гэж үзвэл эцсийн график нь Зураг дээр үзүүлсэн хэлбэртэй байна. Хагас мөчлөгийн Фурье тэлэлтийг синусын хувьд авах шаардлагатай тул өмнөх шигээ Фурье коэффициентийг тооцоолно. б

Дурын интервалд зориулсан Фурье цуврал.

L үетэй үечилсэн функцийг өргөтгөх.

Тогтмол функц f(x) нь x нь L-ээр нэмэгдэхэд давтагдана, i.e. f(x+L)=f(x). Өмнө нь авч үзсэн 2π хугацаатай функцээс L үетэй функц руу шилжих нь маш энгийн, учир нь үүнийг хувьсагчийн өөрчлөлтийг ашиглан хийж болно.

-L/2≤x≤L/2 муж дахь f(x) функцийн Фурье цувааг олохын тулд f(x) функц нь u-тай харьцуулахад 2π үетэй байхаар u шинэ хувьсагчийг оруулав. Хэрэв u=2πx/L бол u=-π-ийн хувьд x=-L/2, u=π-ийн хувьд x=L/2. Мөн f(x)=f(Lu/2π)=F(u) гэж үзье. Фурье цуврал F(u) нь хэлбэртэй байна

(Интегралчлалын хязгаарыг L урттай ямар ч интервалаар сольж болно, жишээлбэл, 0-ээс L хүртэл)

L≠2π интервалд заасан функцүүдийн хагас цикл дээрх Фурье цуваа.

u=πх/L орлуулалтын хувьд x=0-ээс x=L хүртэлх интервал нь u=0-ээс u=π хүртэлх интервалтай тохирч байна. Үүний үр дүнд функцийг зөвхөн косинус эсвэл зөвхөн синус хэлбэрээр цуврал болгон өргөжүүлж болно, өөрөөр хэлбэл. В Хагас мөчлөгийн Фурье цуврал.

0-ээс L хүртэлх косинусын тэлэлт нь хэлбэртэй байна

Хэрэв f(x) функц нь а цэгийг агуулсан тодорхой интервал дахь бүх эрэмбийн деривативтай бол түүнд Тейлорын томъёог хэрэглэж болно.
,
Хаана r n– цувралын үлдэгдэл буюу үлдэгдэл гэж нэрлэгддэг бөгөөд үүнийг Лагранжийн томъёогоор тооцоолж болно.
, энд x тоо нь x ба a хооронд байна.

f(x)=

x 0 = цэг дээр Мөрийн элементүүдийн тоо 3 4 5 6 7

задралыг ашиглах үндсэн функцууд e x , cos(x), sin(x), ln(1+x), (1+x) m

Функцийг оруулах дүрэм:

Хэрэв ямар нэг үнэ цэнийн хувьд X r n→ 0 цагт n→∞, тэгвэл хязгаарт Тейлорын томъёо нь энэ утгыг нэгтгэх томьёо болж хувирна Тейлорын цуврал:
,
Иймд f(x) функцийг авч үзэж буй x цэг дээрх Тейлорын цуврал болгон өргөжүүлж болно, хэрэв:
1) бүх захиалгын деривативтай;
2) баригдсан цуваа энэ цэг дээр нийлнэ.

a = 0 үед бид нэртэй цувралыг авна Маклаурины ойролцоо:
,
Маклаурин цувралын хамгийн энгийн (анхны) функцүүдийн өргөтгөл:
Экспоненциал функцууд
, R=∞
Тригонометрийн функцууд
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
actgx функц нь х-ийн зэрэглэлээр тэлэхгүй, учир нь ctg0=∞
Гиперболын функцууд


Логарифм функцууд
, -1
Бином цуврал
.

Жишээ №1. Функцийг чадлын цуврал болгон өргөжүүлнэ үү f(x)= 2x.
Шийдэл. Функцийн утгууд ба түүний деривативуудыг олъё X=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2= ln2;
f""(x) = 2x ln 2 2, f""( 0) = 2 0 ln 2 2= ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
Деривативын олж авсан утгыг Тейлорын цуврал томъёонд орлуулснаар бид дараахь зүйлийг олж авна.

Энэ цувралын нэгдэх радиус нь хязгааргүйтэй тэнцүү тул энэ өргөтгөл нь -∞-д хүчинтэй байна.<x<+∞.

Жишээ №2. Тейлорын цувралыг хүчээр бичнэ үү ( X+4) функцийн хувьд f(x)=д x.
Шийдэл. Функцийн деривативыг олох e xболон тэдний үнэ цэнэ X=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Тиймээс функцийн шаардлагатай Тейлор цуврал нь дараах хэлбэртэй байна.

Энэ өргөтгөл нь -∞-д мөн хүчинтэй<x<+∞.

Жишээ №3. Функцийг өргөжүүлэх f(x)=ln xэрх мэдлийн цувралд ( X- 1),
(өөрөөр хэлбэл, цэгийн ойролцоох Тейлорын цувралд X=1).
Шийдэл. Энэ функцийн деривативуудыг ол.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Эдгээр утгыг томъёонд орлуулснаар бид хүссэн Тейлор цувралыг олж авна.

d'Alembert-ийн тестийг ашиглан цувралууд ½x-1½-д нийлдэг эсэхийг шалгаж болно.<1 . Действительно,

½ бол цуваа нийлнэ X- 1½<1, т.е. при 0<x<2. При X=2 Бид Лейбницийн шалгуурын нөхцлийг хангасан ээлжлэн цуваа олж авна. x=0 үед функц тодорхойлогдоогүй болно. Ийнхүү Тейлорын цувралын нийлэх муж нь хагас задгай интервал (0;2] байна.

Жишээ № 4. Функцийг чадлын цуврал болгон өргөжүүлнэ үү.
Шийдэл. Өргөтгөх (1) -д бид x-г -x 2-оор сольж, бид дараахыг авна.
, -∞

Жишээ №5. Маклаурин цуврал дахь функцийг өргөжүүлэх .
Шийдэл. Бидэнд байна
Томъёо (4) ашиглан бид дараахь зүйлийг бичиж болно.

Томъёонд x-ийн оронд -x-г орлуулснаар бид дараахь зүйлийг авна.

Эндээс бид олдог: ln(1+x)-ln(1-x) = -
Хаалтуудыг нээж, цувралын нөхцлүүдийг дахин цэгцэлж, ижил төстэй нэр томъёог авчрахад бид олж авна
. Энэ цуваа нь (-1;1) интервалд нийлдэг, учир нь энэ интервалд нийлдэг хоёр цувралаас авсан.

Сэтгэгдэл .
Формула (1)-(5) нь харгалзах функцуудыг Тейлорын цуврал болгон өргөжүүлэхэд ашиглаж болно, жишээлбэл. эерэг бүхэл тоонд функцийг өргөтгөхөд ( Ха). Үүнийг хийхийн тулд (1)-(5) функцүүдийн аль нэгийг авахын тулд өгөгдсөн функц дээр ижил төстэй хувиргалтыг хийх шаардлагатай. Xзардал k( Ха) m , k нь тогтмол тоо, m нь эерэг бүхэл тоо юм. Хувьсагчийн өөрчлөлт хийх нь ихэвчлэн тохиромжтой байдаг т=Хамөн Маклаурины цуврал дахь t-тэй холбоотой үүссэн функцийг өргөжүүлнэ.

Энэ арга нь чадлын цуваа дахь функцийн тэлэлтийн өвөрмөц байдлын тухай теорем дээр суурилдаг. Энэ теоремын мөн чанар нь нэг цэгийн ойролцоо түүний тэлэлт хэрхэн хийгдсэнээс үл хамааран ижил функцэд нийлэх хоёр өөр чадлын цуваа олж авах боломжгүй юм.

Жишээ № 5a. Маклаурины цуврал дахь функцийг өргөжүүлж, нийлэх мужийг заана уу.
Шийдэл. Эхлээд бид 1-x-6x 2 =(1-3x)(1+2x) , .
бага ангид:

3/(1-3x) бутархайг 3х хуваарьтай хязгааргүй буурах геометр прогрессийн нийлбэр гэж үзэж болно, хэрэв |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

нийлэх мужтай |x|< 1/3.

Жишээ № 6. Функцийг x = 3 цэгийн ойролцоо Тейлорын цуврал болгон өргөжүүл.
Шийдэл. Энэ асуудлыг өмнөх шигээ Тейлорын цувралын тодорхойлолтыг ашиглан шийдэж болох бөгөөд үүний тулд функцийн дериватив ба тэдгээрийн утгыг олох хэрэгтэй. X=3. Гэсэн хэдий ч одоо байгаа өргөтгөлийг ашиглах нь илүү хялбар байх болно (5):
=
Үүссэн цуваа нь буюу -3-т нийлдэг

Жишээ № 7. Тейлорын цувралыг ln(x+2) функцийн (x -1) зэрэглэлээр бич.
Шийдэл.


Цуврал нь , эсвэл -2-д нийлдэг< x < 5.

Жишээ № 8. f(x)=sin(πx/4) функцийг x =2 цэгийн ойролцоох Тейлорын цуваа болгон өргөжүүл.
Шийдэл. t=x-2 орлуулалтыг хийцгээе:

Бид x-ийн оронд π / 4 t-ийг орлуулах өргөтгөлийг (3) ашигласнаар бид дараахь зүйлийг олж авна.

Үүссэн цуваа нь өгөгдсөн функцэд -∞ дээр нийлдэг< π / 4 t<+∞, т.е. при (-∞Тиймээс,
, (-∞

Хүчний цуваа ашиглан ойролцоогоор тооцоолол

Эрчим хүчний цувааг ойролцоогоор тооцоололд өргөн ашигладаг. Тэдгээрийн тусламжтайгаар та үндэс, тригонометрийн функц, тоон логарифм, тодорхой интегралын утгыг өгөгдсөн нарийвчлалтайгаар тооцоолж болно. Дифференциал тэгшитгэлийг интеграци хийх үед цувралыг бас ашигладаг.
Хүч чадлын цуваа дахь функцийн өргөтгөлийг авч үзье.

Өгөгдсөн цэг дэх функцийн ойролцоо утгыг тооцоолохын тулд X, заасан цувралын нэгдэх бүсэд хамаарах эхнийх нь түүний өргөтгөлийн хэсэгт үлддэг. nгишүүд ( n- хязгаарлагдмал тоо), үлдсэн нэр томъёог хасна:

Олж авсан ойролцоо утгын алдааг тооцоолохын тулд хаясан үлдэгдлийг тооцоолох шаардлагатай rn (x) . Үүнийг хийхийн тулд дараах техникийг ашиглана уу.

• Хэрэв үр дүнгийн цуваа ээлжлэн байгаа бол дараах шинж чанарыг ашиглана. Лейбницийн нөхцөлийг хангасан ээлжлэн цувааны хувьд үнэмлэхүй утгын цувралын үлдсэн хэсэг нь хасагдсан эхний гишүүнээс хэтрэхгүй байна..
• хэрэв өгөгдсөн цуваа тогтмол тэмдэгтэй бол хасагдсан гишүүдээс бүрдсэн цувааг хязгааргүй буурах геометр прогресстой харьцуулна.
• ерөнхий тохиолдолд, Тейлорын цувралын үлдэгдлийг тооцоолохын тулд та Лагранжийн томъёог ашиглаж болно: a x ).

Жишээ №1. ln(3)-ийг 0.01-ийн нарийвчлалтайгаар тооцоол.
Шийдэл. x=1/2 гэсэн өргөтгөлийг ашиглая (өмнөх сэдэв дэх жишээ 5-ыг үзнэ үү):

Үүнийг хийхийн тулд өргөтгөлийн эхний гурван гишүүний дараа үлдэгдлийг хаяж чадах эсэхийг шалгая, бид үүнийг хязгааргүй буурдаг геометрийн прогрессийн нийлбэрээр үнэлэх болно.

Тиймээс бид энэ үлдэгдлийг хаяж, авах боломжтой

Жишээ №2. 0.0001-ийн нарийвчлалтайгаар тооцоол.
Шийдэл. Хоёр гишүүний цувааг ашиглая. 5 3 нь 130-тай хамгийн ойр бүхэл тооны шоо учраас 130-ын тоог 130 = 5 3 +5 гэж илэрхийлэх нь зүйтэй.



Учир нь Лейбницийн шалгуурыг хангасан ээлжит цувралын дөрөв дэх гишүүн нь шаардлагатай нарийвчлалаас бага байна:
, тиймээс үүнийг болон түүний дараах нэр томъёог хаяж болно.
Практикт шаардлагатай олон тодорхой буюу буруу интегралыг Ньютон-Лейбницийн томьёог ашиглан тооцоолох боломжгүй, учир нь түүний хэрэглээ нь үндсэн функцүүдэд илэрхийлэлгүй эсрэг деривативыг олохтой холбоотой байдаг. Эсрэг дериватив олох боломжтой боловч энэ нь шаардлагагүй хөдөлмөр шаарддаг. Харин интеграл функцийг зэрэглэлийн цуваа болгон өргөтгөж, интегралын хязгаар нь энэ цувралын нийлэх интервалд хамаарах бол урьдчилан тодорхойлсон нарийвчлалтайгаар интегралын ойролцоо тооцоолол хийх боломжтой.

Жишээ №3. ∫ 0 1 4 sin (x) x интегралыг 10 -5 дотор тооцоол.
Шийдэл. Харгалзах тодорхойгүй интегралыг энгийн функцээр илэрхийлэх боломжгүй, өөрөөр хэлбэл. "байнгын бус интеграл"-ыг илэрхийлнэ. Ньютон-Лейбницийн томъёог энд хэрэглэх боломжгүй. Интегралыг ойролцоогоор тооцоолъё.
Нүглийн цувралыг нэр томъёогоор хуваах xдээр x, бид авах:

Энэ цувралыг нэр томъёогоор нэгтгэж (интеграцийн хязгаар нь энэ цувралын нийлэх интервалд хамаарах тул энэ нь боломжтой) бид дараахь зүйлийг олж авна.

Үүссэн цуваа нь Лейбницийн нөхцлийг хангаж байгаа тул өгөгдсөн нарийвчлалтайгаар хүссэн утгыг авахын тулд эхний хоёр гишүүний нийлбэрийг авахад хангалттай.
Тиймээс бид олдог
.

Жишээ № 4. ∫ 0 1 4 e x 2 интегралыг 0.001 нарийвчлалтайгаар тооцоол.
Шийдэл.
. Үр дүнгийн цувралын хоёр дахь гишүүний дараа үлдэгдлийг хаяж чадах эсэхийг шалгацгаая.
0.0001<0.001. Следовательно, .

Хэрэв функц f(x)цэгийг агуулсан зарим интервалтай байна А, бүх дарааллын дериватив, дараа нь Тэйлорын томъёог түүнд хэрэглэж болно:

Хаана r n– цувралын үлдэгдэл буюу үлдэгдэл гэж нэрлэгддэг бөгөөд үүнийг Лагранжийн томъёогоор тооцоолж болно.

, энд x тоо хоёрын хооронд байна XТэгээд А.

Хэрэв ямар нэг үнэ цэнийн хувьд x r n®0 цагт n®¥, тэгвэл хязгаарт Тейлорын томъёо нь энэ утгыг нэгтгэх томьёо болж хувирна Тейлорын цуврал:

Тиймээс функц f(x)тухайн цэг дээр Тейлорын цуврал болгон өргөжүүлж болно X, Хэрэв:

1) бүх захиалгын деривативтай;

2) баригдсан цуваа энэ цэг дээр нийлнэ.

At А=0 гэж нэрлэгддэг цуврал гарч ирнэ Маклаурины ойролцоо:

Жишээ 1 f(x)= 2x.

Шийдэл. Функцийн утгууд ба түүний деривативуудыг олъё X=0

f(x) = 2x, f( 0) = 2 0 =1;

f¢(x) = 2x ln2, f¢( 0) = 2 0 ln2= ln2;

f¢¢(x) = 2x ln 2 2, f¢¢( 0) = 2 0 ln 2 2= ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.

Деривативын олж авсан утгыг Тейлорын цуврал томъёонд орлуулснаар бид дараахь зүйлийг олж авна.

Энэ цувралын нэгдэх радиус нь хязгааргүйтэй тэнцүү тул энэ өргөтгөл нь -¥-д хүчинтэй байна.<x<+¥.

Жишээ 2 X+4) функцийн хувьд f(x)=д x.

Шийдэл. Функцийн деривативыг олох e xболон тэдний үнэ цэнэ X=-4.

f(x)= e x, f(-4) = e -4 ;

f¢(x)= e x, f¢(-4) = e -4 ;

f¢¢(x)= e x, f¢¢(-4) = e -4 ;

f(n)(x)= e x, f(n)( -4) = e -4 .

Тиймээс функцийн шаардлагатай Тейлор цуврал дараах хэлбэртэй байна.

Энэ өргөтгөл нь -¥-д мөн хүчинтэй<x<+¥.

Жишээ 3 . Функцийг өргөжүүлэх f(x)=ln xэрх мэдлийн цувралд ( X- 1),

(өөрөөр хэлбэл, цэгийн ойролцоох Тейлорын цувралд X=1).

Шийдэл. Энэ функцийн деривативуудыг ол.

Эдгээр утгыг томъёонд орлуулснаар бид хүссэн Тейлор цувралыг олж авна.

d'Alembert-ийн тестийг ашигласнаар цувралууд хэзээ нэгдэж байгааг шалгаж болно

½ X- 1½<1. Действительно,

½ бол цуваа нийлнэ X- 1½<1, т.е. при 0<x<2. При X=2 Бид Лейбницийн шалгуурын нөхцлийг хангасан ээлжлэн цуваа олж авна. At X=0 функц тодорхойлогдоогүй байна. Ийнхүү Тейлорын цувралын нийлэх муж нь хагас задгай интервал (0;2] байна.

Энэ аргаар олж авсан өргөтгөлүүдийг Маклаурин цувралд (жишээ нь цэгийн ойролцоо) танилцуулъя. X=0) зарим энгийн функцүүдийн хувьд:

(2) ,

(3) ,

(сүүлчийн задрал гэж нэрлэдэг бином цуврал)

Жишээ 4 . Функцийг чадлын цуврал болгон өргөжүүлнэ үү

Шийдэл. Өргөтгөх хэсэгт (1) бид солино Xдээр - X 2, бид авна:

Жишээ 5 . Маклаурин цуврал дахь функцийг өргөжүүлэх

Шийдэл. Бидэнд байна

Томъёо (4) ашиглан бид дараахь зүйлийг бичиж болно.

оронд нь орлуулах Xтомъёонд оруулна -Х, бид авах:

Эндээс бид олж мэднэ:

Хаалтуудыг нээж, цувралын нөхцлүүдийг дахин цэгцэлж, ижил төстэй нэр томъёог авчрахад бид олж авна

Энэ цуврал интервалд нийлдэг

(-1;1), учир нь тус бүр нь энэ интервалд нийлдэг хоёр цувралаас авсан.

Сэтгэгдэл .

Формула (1)-(5) нь харгалзах функцуудыг Тейлорын цуврал болгон өргөжүүлэхэд ашиглаж болно, жишээлбэл. эерэг бүхэл тоонд функцийг өргөтгөхөд ( Ха). Үүнийг хийхийн тулд (1)-(5) функцүүдийн аль нэгийг авахын тулд өгөгдсөн функц дээр ижил төстэй хувиргалтыг хийх шаардлагатай. Xзардал k( Ха) m , k нь тогтмол тоо, m нь эерэг бүхэл тоо юм. Хувьсагчийн өөрчлөлт хийх нь ихэвчлэн тохиромжтой байдаг т=Хамөн Маклаурины цуврал дахь t-тэй холбоотой үүссэн функцийг өргөжүүлнэ.

Энэ арга нь функцын зэрэглэлийн цуваа тэлэлтийн өвөрмөц байдлын тухай теоремыг харуулж байна. Энэ теоремын мөн чанар нь нэг цэгийн ойролцоо түүний тэлэлт хэрхэн хийгдсэнээс үл хамааран ижил функцэд нийлэх хоёр өөр чадлын цуваа олж авах боломжгүй юм.

Жишээ 6 . Тейлорын цувралын функцийг цэгийн ойролцоо өргөжүүл X=3.

Шийдэл. Энэ асуудлыг өмнөх шигээ Тейлорын цувралын тодорхойлолтыг ашиглан шийдэж болох бөгөөд үүний тулд функцийн дериватив ба тэдгээрийн утгыг олох хэрэгтэй. X=3. Гэсэн хэдий ч одоо байгаа өргөтгөлийг ашиглах нь илүү хялбар байх болно (5):

Үр дүнд нь цуваа нийлдэг эсвэл -3<х- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Жишээ 7 . Тейлорын цувралыг хүчээр бичнэ үү ( X-1) функцууд .

Шийдэл.

Цуврал нэгдэн нийлдэг , эсвэл -2< x£5.

Функциональ цувралын онолын хувьд функцийг цуврал болгон өргөжүүлэхэд зориулагдсан хэсэг нь гол байрыг эзэлдэг.

Тиймээс даалгавар нь тавигдсан: өгөгдсөн функцийн хувьд Бид ийм хүчирхэг цуваа олох хэрэгтэй

тодорхой интервал дээр нийлж, нийлбэр нь тэнцүү байв
, тэдгээр.

= ..

Энэ даалгавар гэж нэрлэдэг функцийг чадлын цуваа болгон өргөжүүлэх асуудал.

Хүчтэй цуваа дахь функцийг задлах зайлшгүй нөхцөлТүүний ялгах чадвар нь хязгааргүй олон удаа байдаг - энэ нь нийлэг хүчний цувааны шинж чанараас гардаг. Энэ нөхцөл нь дүрмээр бол тэдгээрийн тодорхойлолтын хүрээнд үндсэн функцүүдийн хувьд хангагдана.

Тиймээс функц гэж үзье
ямар ч дарааллын деривативтай. Үүнийг хүчирхэг цуврал болгон өргөжүүлэх боломжтой юу, хэрэв тийм бол бид энэ цувралыг хэрхэн олох вэ? Асуудлын хоёр дахь хэсгийг шийдвэрлэхэд хялбар тул үүнээс эхэлцгээе.

функц гэж үзье
цэгийг агуулсан интервалд нийлдэг хүчний цувааны нийлбэрээр илэрхийлж болно X 0 :

= .. (*)

Хаана А 0 , А 1 , А 2 ,...,А n ,... – үл мэдэгдэх (хараахан) коэффициентүүд.

Тэгш (*) утгыг оруулъя x = x 0 , тэгвэл бид авна

.

Хүчний цуваа (*) гишүүнийг гишүүнээр нь ялгаж үзье

= ..

мөн энд итгэж байна x = x 0 , бид авдаг

.

Дараагийн ялгаагаар бид цувралыг олж авна

= ..

итгэх x = x 0 , бид авдаг
, хаана
.

Дараа нь n-Бид олон янзын ялгааг олж авдаг

Сүүлийн тэгш байдлыг харгалзан үзвэл x = x 0 , бид авдаг
, хаана

Тиймээс коэффициентүүд олддог

,
,
, …,
,….,

аль цувралд (*) орлуулснаар бид авна

Үр дүнд нь цуврал гэж нэрлэдэг Тейлорын хажууд функцийн хувьд
.

Тиймээс бид үүнийг тогтоосон хэрэв функцийг хүчирхэг цуврал болгон өргөжүүлж чадвал (x - x 0 ), тэгвэл энэ өргөтгөл нь өвөрмөц бөгөөд үр дүнд нь гарсан цуврал нь заавал Тейлорын цуврал байх болно.

Тухайн цэг дээр дурын эрэмбийн деривативтай ямар ч функцийн хувьд Тейлорын цувралыг авч болно гэдгийг анхаарна уу x = x 0 . Гэхдээ энэ нь функц ба үр дүнгийн цувааны хооронд тэнцүү тэмдгийг байрлуулж болно гэсэн үг биш юм. цувралын нийлбэр нь анхны функцтэй тэнцүү байна. Нэгдүгээрт, ийм тэгш байдал нь зөвхөн нийлэх мужид л утга учиртай байх ба функцийн хувьд олж авсан Тейлорын цуваа зөрөөтэй байж болно, хоёрдугаарт, хэрэв Тейлорын цуваа нийлдэг бол түүний нийлбэр нь анхны функцтэй давхцахгүй байж болно.

3.2. Тейлорын цуврал дахь функцийг задлах хангалттай нөхцөл

Даалгаврыг шийдвэрлэхэд туслах мэдэгдлийг боловсруулцгаая.

Хэрэв функц
x цэгийн зарим хөршид 0 хүртэл деривативтай (n+ 1) дарааллаар хамааруулсан, дараа нь энэ хөршид бид байнатомъёо Тейлор

ХаанаР n (X)-Тэйлорын томъёоны үлдсэн гишүүн нь (Лагранж хэлбэр) хэлбэртэй байна.

Хаана цэгξ x ба x хооронд оршдог 0 .

Тейлорын цуврал ба Тейлорын томъёоны хооронд ялгаа байгааг анхаарна уу: Тейлорын томъёо нь хязгаарлагдмал нийлбэр, i.e. p -тогтмол тоо.

Цувралын нийлбэр гэдгийг санаарай С(x) хэсэгчилсэн нийлбэрүүдийн функциональ дарааллын хязгаар гэж тодорхойлж болно С n (x) тодорхой интервалаар X:

.

Үүний дагуу функцийг Тейлорын цуврал болгон өргөжүүлэх нь аль ч цувралыг олох гэсэн үг юм XX

Тейлорын томъёог хаана гэсэн хэлбэрээр бичье

Үүнийг анхаарна уу
бидний олж авсан алдааг тодорхойлж, функцийг солино е(x) олон гишүүнт С n (x).

Хэрэв
, Тэр
, тэдгээр. функцийг Тейлорын цуврал болгон өргөжүүлсэн. Харин эсрэгээр, хэрэв
, Тэр
.

Ингээд бид нотолсон Тейлорын цуврал дахь функцийн задралын шалгуур.

Функцийн хувьде(x) нь Тейлорын цуваа болж өргөжиж, энэ интервалд шаардлагатай бөгөөд хангалттай
, ХаанаР n (x) нь Тейлорын цувралын үлдсэн гишүүн юм.

Томъёолсон шалгуурыг ашиглан хүн олж авах боломжтой хангалттайТейлорын цуврал дахь функцийн задралын нөхцөл.

Хэрэв орволx цэгийн зарим хөрш 0 функцийн бүх деривативуудын үнэмлэхүй утгууд нь ижил M тоогоор хязгаарлагддаг≥ 0, өөрөөр хэлбэл.

, Тo энэ хэсэгт функц нь Тейлорын цуврал болж өргөждөг.

Дээрхээс харахад дараах байдалтай байна алгоритмфункцийг өргөжүүлэх е(x) Тейлорын цувралдцэгийн ойролцоо X 0 :

1. Функцийн деривативыг олох е(x):

f(x), f’(x), f”(x), f’”(x), f (n) (x),…

2. Функцийн утга ба түүний деривативын утгыг цэг дээр тооцоол X 0

f(x 0 ), f’(x 0 ), f"(x 0 ), f'"(x 0 ), f (n) (х 0 ),…

3. Бид Тейлорын цувааг албан ёсоор бичиж, үүссэн чадлын цувааны нийлэх мужийг олно.

4. Бид хангалттай нөхцлийн биелэлтийг шалгадаг, i.e. үүний төлөө бид тогтоодог Xнийлэх мужаас, үлдэгдэл хугацаа Р n (x) гэж тэглэх хандлагатай байна
эсвэл
.

Энэ алгоритмыг ашиглан функцуудыг Тейлорын цуврал болгон өргөжүүлэхийг нэрлэдэг Тодорхойлолтоор функцийг Тейлорын цуврал болгон өргөжүүлэхэсвэл шууд задрал.