Аксиомы планиметрии:

В различных учебниках свойства прямых и плоскостей могут быть представлены по-разному, в виде аксиомы, следствия из нее, теоремы, леммы и т.д. Рассмотрим учебник Погорелова А.В.

Прямая разбивает плоскость на две полуплоскости.

0

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Аксиомы стереометрии:

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие этой плоскости, и точки не принадлежащие ей.

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

Из трех точек на прямой одна и только одна лежит между двумя другими.

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 0 . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.

На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Сечение

В пространстве две фигуры, для нашего случая плоскость и многогранник могут иметь следующее взаимное расположение: не пересекаются, пересекаются в точке, пересекаются по прямой и плоскость пересекает многогранник по его внутренности (рис.1), и при этом образуют следующие фигуры:

а) пустая фигура (не пересекаются)

б) точка

в) отрезок

г) многоугольник

Если в пересечении многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника с плоскостью .

рис.1

Определение. Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела с плоскостью.

Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.

Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом, пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок.

Если плоскости пересекаются по прямой, то прямую называют следом одной из этих плоскостей на другой.

В общем случае секущая плоскость многогранника пересекает плоскость каждой его грани (а также любую другую секущую плоскость этого многогранника). Она пересекает и каждую из прямых, на которых лежат ребра многогранника.

Прямую, по которой секущая плоскость пересекает плоскость какой-либо грани многогранника, называют следом секущей плоскости на плоскости этой грани, а точку, в которой секущая плоскость пересекает прямую, содержащую какое – либо ребро многогранника, называют следом секущей плоскости на этой прямой. Эта точка является и следом прямой на секущей плоскости. Если секущая плоскость пересекает непосредственно грань многогранника, то можно говорить о следе секущей плоскости на грани, и, аналогично, о следе секущей плоскости на ребре многогранника, то есть о следе ребра на секущей плоскости.

Так как прямая однозначно определяется двумя точками, то для нахождения следа секущей плоскости на любой другой плоскости и, в частности, на плоскости любой грани многогранника, достаточно построить две общие точки плоскостей

Для построения следа секущей плоскости, а также для построения сечения многогранника этой плоскостью, должен быть задан не только многогранник, но и секущая плоскость. А построение плоскости сечения проходит в зависимости от задания этой плоскости. Основными способами задания плоскости, и в частности секущей плоскости, являются следующие:

тремя точками не лежащих на одной прямой;

прямой и не лежащей на ней точкой;

двумя параллельными прямыми;

двумя пересекающимися прямыми;

точкой и двумя скрещивающимися прямыми;

Возможны и другие способы задания секущей плоскости.

Поэтому все способы построения сечений многогранников можно разделить на методы.

Методы построения сечений многогранников

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Существует три основных метода построения сечений многогранников:

Аксиоматический метод:

Метод следов.

Комбинированный метод.

Координатный метод.

Заметим , что метод следов и метод вспомогательных сечений являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

построение сечения, проходящего через заданную прямую параллельно, другой заданной прямой;

построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;

построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;

построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

Основными действиями, составляющие методы построения сечений, являются нахождение точки пересечения прямой с плоскостью, построения линии пересечения двух плоскостей, построение прямой параллельной плоскости, перпендикулярной плоскости. Для построения прямой пересечения двух плоскостей обычно находят две ее точки и проводят через них прямую. Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную. Тогда искомая точка получается в пересечении найденной прямой с данной.

Рассмотрим отдельно перечисленные нами методы построения сечений многогранников:

Метод следов.

Метод следов основывается (операеться) на аксиомах стереометрии, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют основным следом секущей плоскости . Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.

Отметим, что при построении основного следа секущей плоскости используется следующее утверждение.

Если точки принадлежат секущей плоскости и не лежат на одной прямой, а их проекция (центральными или параллельными) на плоскость, выбранную в качестве основной, являются соответственно точки то точки пересечения соответственных прямых, то есть точки и лежат на одной прямой (рис.1, а, б).

рис.1.а рис.1.б

Эта прямая является основным следом секущей плоскости. Так как точки лежат на основном следе, то для его построения достаточно найти две точки из этих трех.

Метод вспомогательных сечений.

Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее, в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Комбинированный метод

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Координатный метод построения сечений.

Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.

Заметим , что это способ построения сечения многогранника приемлем для компьютера, так как он связан с большим объемом вычислений и поэтому этот метод целесообразно реализовать с помощью ЭВМ.

Наша основная задача будет состоять в построении сечения многогранника с плоскостью, т.е. в построении пересечения этих двух множеств.

Построение сечений многогранников

Прежде всего заметим, что сечение выпуклого многогранника есть выпуклый плоский многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многогранника, а стороны с его гранями.

Примеры построения сечений:

Способы задания сечения весьма разнообразны. Наиболее распространенным из них является способ задания секущей плоскости тремя точками, не лежащими на одной прямой.

Пример 1. Для параллелепипеда ABCDA 1 B 1 C 1 D 1 . Построить сечение проходящее через точки M, N, L.

Решение:

Соединим точки M и L, лежащие в плоскости AA 1 D 1 D.

Пересечем прямую ML (принадлежащую сечению) с ребром A 1 D 1 1 D 1 D. Получим точку X 1 .

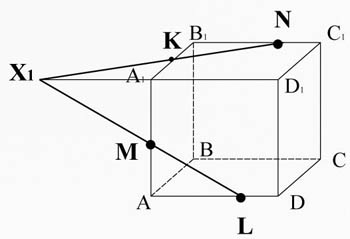
Точка X1 лежит на ребре A 1 D 1 , а значит и плоскости A 1 B 1 C 1 D 1 , соединим ее сточкой N, лежащей в этой же плоскости.

X 1 N пересекается с ребром A 1 B 1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA 1 B 1 B.

Найдем прямую пересечения плоскости сечения с плоскостью DD 1 C 1 C:

Пересечем прямую ML (принадлежащую сечению) с ребром DD 1 , они лежат в одной плоскости AA 1 D 1 D, получим точку X 2 .

Пересечем прямую KN (принадлежащую сечению) с ребром D 1 C 1 , они лежат в одной плоскости A 1 B 1 C 1 D 1 , получим точку X3;

Точки X2 и X3 лежат в плоскости DD 1 C 1 C. Проведем прямую X 2 X 3 , которая пересечет ребро C 1 C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника, что и мы сделали. MKNTPL - искомое сечение.

Заметим. Эту же самую задачу на построение сечения, можно решить воспользуевавшийся свойством параллельных плоскостей.

Из выше сказанного можно составить алгоритм (правило) решения задач, данного типа.

Правила построения сечений многогранников:

1. проводим прямые через точки, лежащие в одной плоскости;

   ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:

Пример 2. D L , M

Решим аксиоматическим методом:

Проведем вспомогательную плоскость DKM , которая пересекает ребра АВ и ВС в точках Е и F (ход решение на рис 2.). Построим «след» КМ плоскости сечения на этой вспомогательной плоскости, найдем точку пересечения КМ и Е F – точку Р. Точка Р, как и L , лежит в плоскости АВС, и можно провести прямую, по которой плоскость сечения пересекает плоскость АВС(«след» сечения в плоскости АВС).

Пример 3. На ребрах AB и AD пирамиды MABCD зададим соответственно точки P и Q - середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Решение проведем комбинированным методом:

1). Ясно, что основным следом плоскости PQR является прямая PQ.

2). Найдем точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.

3). Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.

4). Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ - средняя линия треугольника ABD, то PQ параллена BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.

5). Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD"RB" - искомое сечение

Рассмотрим сечения призмы для простоты, то есть удобства логических размышлений рассмотрим сечения куба (рис.3.а):

Рис. 3.а

Сечения призмы плоскостями, параллельными боковым ребрам, является параллелограммами. В частности, параллелограммами являются диагональные сечения (рис. 4).

Опр. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Многоугольник, получающийся при диагональном сечении призмы, является параллелограммом. Вопрос о числе диагональных сечений n -угольной призмы труднее, чем вопрос о числе диагоналей. Сечений будет столько же сколько диагоналей у основания. Мы знаем, что у выпуклой призмы в основаниях – выпуклые многоугольники, а у выпуклого n -угольника диагоналей. И так можно говорить, что диагональных сечений вдвое меньше, чем диагоналей.

Заметим: При построении сечений параллелепипеда на рисунке следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким – то отрезкам, то эти отрезки параллельны «по свойству параллелепипеда т.е. противоположные грани параллелепипеда параллельны и равны.»

Дадим ответы на часто возникающие вопросы:

Какие многоугольники получаются в сечении куба плоскостью?

«треугольник, четырехугольник, пятиугольник, шестиугольник ».

Может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник?

«не могут».

3)Возникает вопрос чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника .

Пример 3. Построить сечение призмы A 1 B 1 C 1 D 1 ABCD плоскостью, проходящей через три точки M, N, K.

Рассмотрим случай расположения точек M, N, K на поверхности призмы (рис. 5).

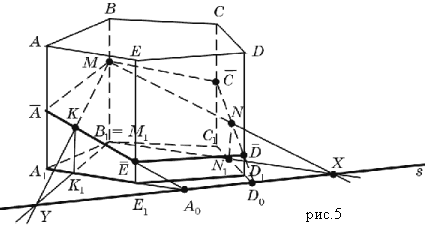
Рассмотрим случай: В данном случае очевидно, что M1 = B1.

Построение:

Пример 4. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.6)).

Решение:

Рис. 6

Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х.

Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.

Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.

Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два не соседних боковых ребра пирамиды.

Пример 4. Построить сечение пирамиды АВС D плоскостью, проходящей через точки К, L , M .

Решение:

1. Проведем еще одну вспомогательную плоскость DCK и построим точку пересечения В L и D К – точку Е. Эта точка принадлежит обеим вспомогательным плоскостям (рис. 7, б);

   Найдем точку пересечения отрезков LM и ЕС (эти отрезки лежат в плоскости BLC , рис.7, в) – точку F . Точка F лежит в плоскости сечения и в плоскости DCK ;

   Проведем прямую KF и найдем точку пересечения этой прямой с DC – точку N (точка N принадлежит сечению). Четырехугольник KLNM – искомое сечение.

Этот же пример решим по другому .

Допустим что по точкам К, L , и М построено сечение KLNM (рис. 7). Обозначим через F точку пересечения диагоналей четырехугольника KLNM . Проведем прямую DF и обозначим через F 1 ее точку пересечения с гранью АВС. Точка F 1 совпадает с точкой пересечения прямых АМ и СК (F 1 одновременно принадлежит плоскостям АМ D и D СК). Точку F 1 легко построить. Далее строим точку F как точку пересечения DF 1 и LM . Далее находим точку N .

Рассмотренный прием называют методом внутреннего проектирования . (Для нашего случая речь идет о центральном проектировании. Четырехугольник K МСА есть проекция четырехугольника KMNL из точки D . При этом точка пересечения диагоналей KMNL – точка F – переходит в точку пересечения диагоналей четырехугольника K МСА – точку F 1 .

Площадь сечения многогранника.

Задача на вычисление площади сечения многогранника обычно решается в несколько этапов. Если в задаче говориться, что сечение построено (или что секущая плоскость проведена и т.п.), то на первом этапе решения выясняют вид фигуры полученной в сечении.

Это необходимо сделать, чтобы выбрать соответствующую формулу для вычисления площади сечения. После того как вид фигуры, полученной в сечении, выяснен и выбрана формула для подсчета площади этой фигуры, переходят непосредственно к вычислительной работе.

В некоторых случаях может оказаться проще, если, не выясняя вида фигуры, полученной в сечении, перейти сразу к вычислениям ее площади по формуле, которая следует из теоремы.

Теорема о площади ортогональной проекции многоугольника: площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: .

Справедлива формула для вычисления площади сечения: где это площадь ортогональной проекции фигуры, полученной в сечении, аэто угол между секущей плоскостью и плоскостью, на которую фигура спроектирована. При таком ходе решения необходимо построить ортогональную проекцию фигуры, полученной в сечении, и подсчитать

Если в условии задачи говориться, что сечение требуется построить и найти площадь полученного сечения, то на первом этапе следует обосновано выполнить построение заданного сечения, и затем, естественно, определить вид фигуры, полученной в сечении, и т.д.

Отметим следующий факт: так как строятся сечения выпуклых многогранников, то многоугольник сечения будет тоже выпуклым, поэтому его площадь можно найти разбиением на треугольники, то есть площадь сечения равна сумме площадей треугольников из которых оно составлено.

Задача 1.

– правильная треугольная пирамида со стороной основания равной и высотой равной Постройте сечение пирамиды плоскостью, проходящей через точки, где – середина стороны, и найдите его площадь (рис.8).

Решение.

Сечением пирамиды является треугольник. Найдем его площадь.

Так как основание пирамиды – равносторонний треугольник и точка – середина стороны, то является высотой и тогда, .

Площадь треугольника можно найти:

Задача 2.

Боковое ребро правильной призмы равно стороне основания. Построить сечения призмы плоскостями, проходящими через точку A , перпендикулярно прямой Если найти площадь полученного сечения призмы.

Решение.

Построим заданное сечение. Сделаем это из чисто геометрических соображений, например, следующим образом.

В плоскости проходящей через заданную прямую и заданную точку проведем через эту точку прямую, перпендикулярную прямой (рис. 9). Воспользуемся с этой целью тем, что в треугольнике то есть его медиана является и высотой этого треугольника. Таким образом, прямая.

Через точку проведем еще одну прямую, перпендикулярную прямой. Проведем ее, например, в плоскости, проходящей через прямую. Ясно, что этой прямой является прямая

Итак, построены две пересекающиеся прямые, перпендикулярные прямой. Этими прямимы определяется плоскость, проходящая через точку перпендикулярно прямой то есть задана секущая плоскость.

Построим сечение призмы этой плоскостью. Заметим, что так как, то прямая параллельна плоскости. Тогда плоскость, проходящая через прямую, пересекает плоскость по прямой, параллельной прямой, то есть и прямой. Проведем через точку прямую и полученную точку соединим точкой.

Четырехугольник заданное сечение. Определим его площадь.

Понятно что четырехугольник является прямоугольником, то есть его площадь

рис. 9

Дмитриев Антон, Киреев Александр

В данной презентации доходчиво, пошагово показаны примеры построения сечений от простых задач к более сложным. Анимация позволяет увидеть этапы построения сечений

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Построение сечений многогранников на примере пр измы ® Создатели: Антон Дмитриев, Киреев Александр. При содействии: Гудковой Ольги Викторовны

План урока Алгоритмы построения сечений Самопроверка Демонстрационные задачи Задачи для закрепления материала

Алгоритмы построения сечений следов параллельных прямых параллельного переноса секущей плоскости внутреннего проектирования комбинированный метод дополнения n -угольной призмы до треугольной призмы Построение сечения методом:

Построение сечения методом следов Основные понятия и умения Построение следа прямой на плоскости Построение следа секущей плоскости Построение сечения

Алгоритм построения сечения методом следов Выяснить имеются ли в одной грани две точки сечения (если да, то через них можно провести сторону сечения). Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом). Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани. Выполнить п.1.

Построение сечения призмы Двух точек принадлежащих одной грани нет. Точка R лежит в плоскости основания. Найдем след прямой KQ на плоскости основания: - KQ ∩K1Q1=T1, T1R- след сечения. 3. T1R ∩CD=E. 4. Проведем EQ. EQ∩DD1=N. 5. Проведем NK. NK ∩AA1=M. 6. Соединяем M и R . Построить сечение плоскостью α , проходящей через точки K,Q,R; K є ADD1, Q є CDD1, R є AB.

Метод параллельных прямых В основу метода положено свойство параллельных плоскостей: «Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Основные умения и понятия Построение плоскости параллельной данной Построение линии пересечения плоскостей Построение сечения

Алгоритм построения сечения методом параллельных прямых. Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q) и их проекции проводим плоскость. Через третью точку (например R) строим параллельную ей плоскость α . Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q . Через точку R проводим прямую а параллельную PQ . Находим точки пересечения прямой а с прямыми m и n. Находим точки пересечения с ребрами соответствующей грани.

(ПРИЗМА) Строим проекции точек P и Q на плоскости верхнего и нижнего оснований. Проводим плоскость P1Q1Q2P2. Через ребро, содержащее точку R, проводим плоскость α параллельную P1Q1Q2. Находим линии пересечения плоскостей ABB1 и CDD1 с плоскость α . Через точку R проводим прямую a||PQ . a∩n=X, a∩m=Y. XP∩AA1=K, XP∩BB1=L; YQ∩CC1=M, YQ∩DD1=N. KLMNR – искомое сечение. Построить сечение плоскостью α , проходящей через точки P,Q,R; P є ABB1, Q є CDD1, R є EE1.

Метод параллельного переноса секущей плоскости Строим вспомогательное сечение данного многогранника, которое удовлетворяет следующим требованиям: оно параллельно секущей плоскости; в пересечении с поверхностью данного многогранника образует треугольник. Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани. Соединяем вершину треугольника с этими точками. Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.

ПРИЗМА R є AA1, P є EDD1, Q є CDD1. Построим вспомогательное сечение AMQ1 ||RPQ. Проведем AM||RP, MQ1||PQ, AMQ1∩ABC=AQ1. P1- проекция точек Р и М на АВС. Проведем Р1В и Р1С. Р1В∩ AQ1=O1, P1C ∩ AQ1=O2. Через точку Р проведем прямые m и n соответственно параллельные МО1 и МО2. m∩BB1=K, n∩CC1=L. LQ∩DD1=T, TP∩EE1=S. RKLTS – искомое сечение Построить сечение призмы плоскостью α , проходящей через точки P,Q,R; P є EDD1, Q є CDD1, R є AA1 .

Алгоритм построения сечения методом внутреннего проектирования. Построить вспомогательные сечения и найти линию их пересечения. Построить след сечения на ребре многогранника. Если точек сечения не хватает для построения самого сечения повторить пп.1-2.

Построение вспомогательных сечений. ПРИЗМА Параллельное проектирование.

Построение следа сечения на ребре

Комбинированный метод. Через вторую прямую q и какую-нибудь точку W первой прямой р провести плоскость β . В плоскости β через точку W провести прямую q‘ параллельную q . Пересекающимися прямыми p и q‘ определяется плоскость α . Непосредственное построение сечения многогранника плоскостью α Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом. Применяется для построения сечения многогранника с условием параллельности. 1. Построение сечения многогранника плоскостью α , проходящей через заданную прямую p параллельно другой заданной прямой q .

ПРИЗМА Построить сечение призмы плоскостью α , проходящей через прямую PQ параллельно AE1; P є BE, Q є E1C1. 1. Проведем плоскость через прямую AE1 и точку P. 2. В плоскости AE1P через точку P проведем прямую q" параллельную AE1. q"∩E1S’=K. 3. Пересекающимися прямыми PQ и PK определяется искомая плоскость α. 4. P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V. TVMNL-искомое сечение.

Метод дополнения n -угольной призмы(пирамиды) до треугольной призмы(пирамиды). Данная призма(пирамида) достраивается до треугольной призмы(пирамиды) из тех граней на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение. Строится сечение полученной треугольной призмы(пирамиды). Искомое сечение получается как часть сечения треугольной призмы(пирамиды).

Основные понятия и умения Построение вспомогатель- ных сечений Построение следа сечения на ребре Построение сечения Центральное проектирование Параллельное проектирование

ПРИЗМА Q є BB1C1C, P є AA1, R є EDD1E1. Достраиваем призму до треугольной. Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A 1 E 1 , B 1 C 1 , E 1 D 1. AE ∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1. Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR , используя метод внутреннего проектирования. Это сечение является частью искомого. Строим искомое сечение.

Правило для самоконтроля Если многогранник выпуклый, то сечение выпуклый многоугольник. Вершины многоугольника всегда лежат на ребрах многогранника. Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении. Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении. Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника. Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Базовые задачи на построение сечений многогранников Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей. M є AD, N є DCC1, D1 ; ABCDA1B1C1D1- куб M є ADD1, D1 є ADD1, MD1. D1 є D1DC, N є D1DC, D1N ∩ DC=Q. M є ABC, Q є ABC, MQ. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. M є CC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC. M є DCC1, D1 є DCC1, MD1. A є ABC, K є ABC, AK.

III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла). M є AB, N є AA1, K є A1D1; ABCDA1B1C1D1- куб. NK∩AD=F1 - вершина трехгранного угла образованного плоскостями α , ABC, ADD1. F1M∩CD=F2 - вершина трехгранного угла образованного плоскостями α , ABC, CDD1. F1M ∩BC=P. NK∩DD1=F3 - вершина трехгранного угла образованного плоскостями α , D1DC, ADD1. F3F2∩D1C1=Q, F3F2∩CC1=L. IV. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает ее, то линия пересечения параллельна данной прямой. A1, C, α ||BC1; ABCA1B1C1- призма. α∩ BCC1=n, n||BC1, n∩BB1=S. SA1∩AB=P. Соединяем A1,P и C.

V. Если прямая лежит в плоскости сечения, то точка ее пересечения с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую. M є A1B1C1, K є BCC1, N є ABC; ABCDA1B1C1- параллелепипед. 1 . Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями: α , ABC, MKK1. 2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.

Задачи. На каком рисунке изображено сечение куба плоскостью ABC ? Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться?

Определение

Сечение - это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве” .

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

4. Две плоскости параллельны, если они не имеют общих точек.

5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен \(90^\circ\) .

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

7. Две плоскости называются перпендикулярными, если угол между ними равен \(90^\circ\) .

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

1. Если прямая \(a\) , не лежащая в плоскости \(\pi\) , параллельна некоторой прямой \(p\) , лежащей в плоскости \(\pi\) , то она параллельна данной плоскости.

2. Пусть прямая \(p\) параллельна плоскости \(\mu\) . Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\) , то линия пересечения плоскостей \(\pi\) и \(\mu\) - прямая \(m\) - параллельна прямой \(p\) .

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\) , то линии пересечения плоскостей также параллельны:

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

5. Пусть прямая \(l\) лежит в плоскости \(\lambda\) . Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\) , не лежащей на прямой \(l\) , то прямые \(l\) и \(s\) скрещиваются.

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

7. Теорема о трех перпендикулярах.

Пусть \(AH\) – перпендикуляр к плоскости \(\beta\) . Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\) . Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA"\) и \(BB"\) (точки \(A", B"\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A"B"\) – проекция прямой \(a\) на плоскость \(\mu\) . Точка \(M=a\cap A"B"\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\) .

Причем заметим, что все точки \(A, B, A", B", M\) лежат в одной плоскости.

Пример 1.

Дан куб \(ABCDA"B"C"D"\) . \(A"P=\dfrac 14AA", \ KC=\dfrac15 CC"\) . Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\) .

Решение

1) Т.к. ребра куба \(AA", CC"\) перпендикулярны \((ABC)\) , то точки \(A\) и \(C\) - проекции точек \(P\) и \(K\) . Тогда прямая \(AC\) – проекция прямой \(PK\) на плоскость \(ABC\) . Продлим отрезки \(PK\) и \(AC\) за точки \(K\) и \(C\) соответственно и получим точку пересечения прямых – точку \(E\) .

2) Найдем отношение \(AC:EC\) . \(\triangle PAE\sim \triangle KCE\) по двум углам (\(\angle A=\angle C=90^\circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]

Если обозначить ребро куба за \(a\) , то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\) . Тогда:

\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]

Пример 2.

Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\) , высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\) , считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\) , считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\) .

Решение

1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\) пересечения медиан основания. Найдем проекцию прямой \(MN\) на плоскость \(ABC\) . Т.к. \(DO\perp (ABC)\) , то и \(NO\perp (ABC)\) . Значит, \(O\) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\) . Точка \(Q\) будет лежать на медиане \(AK\) .
Действительно, т.к. \(MQ\) и \(NO\) перпендикулярны \((ABC)\) , то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\) лежат в одной плоскости \(ADK\) , то и точка \(Q\) будет лежать в этой плоскости. Но еще (по построению) точка \(Q\) должна лежать в плоскости \(ABC\) , следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\) .

Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\) . \(L\) – точка пересечения этих прямых.

2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\) , хотя она могла бы лежать и внутри него; а как правильно?).

Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\) . Тогда медиана \(AK=\dfrac{\sqrt3}2a\) . Значит, \(OK=\dfrac13AK=\dfrac 1{2\sqrt3}a\) . Найдем длину отрезка \(OL\) (тогда мы сможем понять, внутри или вне отрезка \(OK\) находится точка \(L\) : если \(OL>OK\) – то вне, иначе – внутри).

а) \(\triangle AMQ\sim \triangle ADO\) по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,

\[\dfrac{MQ}{DO}=\dfrac{AQ}{AO}=\dfrac{MA}{DA}=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1{\sqrt3}a\]

Значит, \(QK=\dfrac{\sqrt3}2a-\dfrac 45\cdot \dfrac 1{\sqrt3}a=\dfrac7{10\sqrt3}a\) .

б) Обозначим \(KL=x\) .
\(\triangle LMQ\sim \triangle LNO\) по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle L\) – общий). Значит,

\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]

Следовательно, \(OL>OK\) , значит, точка \(L\) действительно лежит вне отрезка \(AK\) .

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).

Пример 3

Дана правильная четырехугольная пирамида \(SABCD\) . Найдите сечение пирамиды плоскостью \(\alpha\) , проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\) .

Решение

1) Обозначим середину ребра \(SA\) за \(M\) . Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\) . Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\) .

Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\) , она должна содержать некоторую прямую, параллельную \(BD\) . Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\) . Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) (\(K\in SB, P\in SD\) ). Тогда, соединив точки \(C, P, M, K\) , получим сечение пирамиды плоскостью \(\alpha\) .

2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\) . Таким образом мы полностью определим построенное сечение.

Заметим, что так как \(KP\parallel BD\) , то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\) . Но \(SB=SD\) , значит и \(SK=SP\) . Таким образом, можно найти только \(SP:PD\) .

Рассмотрим \(\triangle ASC\) . \(CM, SH\) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении \(2:1\) , считая от вершины, то есть \(SO:OH=2:1\) .

Теперь по теореме Фалеса из \(\triangle BSD\) : \(\dfrac{SP}{PD}=\dfrac{SO}{OH}=\dfrac21\) .

3) Заметим, что по теореме о трех перпендикулярах \(CO\perp BD\) как наклонная (\(OH\) – перпендикуляр на плоскость \(ABC\) , \(CH\perp BD\) – проекция). Значит, \(CO\perp KP\) . Таким образом, сечением является четырехугольник \(CPMK\) , диагонали которого взаимно перпендикулярны.

Пример 4

Дана прямоугольная пирамида \(DABC\) с ребром \(DB\) , перпендикулярным плоскости \(ABC\) . В основании лежит прямоугольный треугольник с \(\angle B=90^\circ\) , причем \(AB=DB=CB\) . Проведите через прямую \(AB\) плоскость, перпендикулярную грани \(DAC\) , и найдите сечение пирамиды этой плоскостью.

Решение

1) Плоскость \(\alpha\) будет перпендикулярна грани \(DAC\) , если она будет содержать прямую, перпендикулярную \(DAC\) . Проведем из точки \(B\) перпендикуляр на плоскость \(DAC\) - \(BH\) , \(H\in DAC\) .

Проведем вспомогательные \(BK\) – медиану в \(\triangle ABC\) и \(DK\) – медиану в \(\triangle DAC\) .
Т.к. \(AB=BC\) , то \(\triangle ABC\) – равнобедренный, значит, \(BK\) – высота, то есть \(BK\perp AC\) .
Т.к. \(AB=DB=CB\) и \(\angle ABD=\angle CBD=90^\circ\) , то \(\triangle ABD=\triangle CBD\) , следовательно, \(AD=CD\) , следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\) .

Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\) ; наклонная \(BK\perp AC\) , значит и проекция \(HK\perp AC\) . Но мы уже определили, что \(DK\perp AC\) . Таким образом, точка \(H\) лежит на отрезке \(DK\) .

Соединив точки \(A\) и \(H\) , получим отрезок \(AN\) , по которому плоскость \(\alpha\) пересекается с гранью \(DAC\) . Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\) .

2) Определим точное положение точки \(N\) на ребре \(DC\) .

Обозначим \(AB=CB=DB=x\) . Тогда \(BK\) , как медиана, опущенная из вершины прямого угла в \(\triangle ABC\) , равна \(\frac12 AC\) , следовательно, \(BK=\frac12 \cdot \sqrt2 x\) .

Рассмотрим \(\triangle BKD\) . Найдем отношение \(DH:HK\) .

Заметим, что т.к. \(BH\perp (DAC)\) , то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\) . Тогда \(\triangle DBH\sim \triangle DBK\) , следовательно

\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]

Рассмотрим теперь \(\triangle ADC\) . Медианы треугольника точной пересечения делятся в отношении \(2:1\) , считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\) .

	Разрез, служащий для выяснения устройства предмета лишь в от-
	дельном, ограниченном месте, называется местным (рис. 24, 25).
			Часть вида и часть соответствующего
			разреза допускается соединять, разделяя их
			сплошной волнистой линией или сплошной
			тонкой линией с изломом (рис. 24).Если при
			этом соединяются половина вида и полови-
			на разреза, каждый из которых является
			симметричной фигурой, то разделяющей
			линией служит ось симметрии. При этом
			ниже оси симметрии (рис. 2, рис. 25).
			Если с осью симметрии изображения
			совпадает какая – либо линия, например,
			проекция ребра (рис. 26), то вид от разреза
	отделяют сплошной волнистой линией, проводимой правее, если ребро изо-
	бражается на виде (рис. 26, а), или левее, если ребро изображается на разрезе
	(рис. 26, б).

Построение сечений

Сечение - изображение фигуры, получающейся при мысленном рассечении предмета плоскостью. На сечении показывается только то, что находится непосредственно в секущей плоскости.

Сечения, не входящие в состав разреза, разделяют на: вынесенные (рис. 27) иналоженные (рис. 28).

Вынесенные сечения являются предпочтительными и их допускается располагать в разрыве между частями одного и того же вида (рис. 29).

Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями, а контур наложенного сечения – сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают (рис. 28).

Ось симметрии вынесенного или наложенного сечения (рис. 28) указывают штрихпунктирной тонкой линией без обозначения буквами и стрелками

и линию сечения не проводят.

В случаях, подобных указанному на рис. 29, при симметричной фигуре сечения, линию сечения не проводят.

Во всех остальных случаях для линии сечения применяют разомкнутую линию с указанием стрелками направления взгляда и обозначают ее одинаковыми прописными буквами русского алфавита. Сечение сопровождают надписью по типу «А – А » (рис. 27).

Для несимметричных сечений, расположенных в разрыве или наложенных (рис. 30), линию сечения проводят со стрелками, но буквами не обозначают. Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстия или углубления в сечении показывают полностью (рис. 31).

Выносные элементы

Выносной элемент - дополнительное отдельное изображение (обычно увеличенное) какой-либо части предмета, требующей графического и других пояснений в отношении формы, размеров и иных данных.

Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию (например, изображение может быть видом, а выносной элемент – разрезом).

При применении выносного элемента соответствующее место отмечают на виде, разрезе или сечении замкнутой сплошной тонкой линией – окружностью, овалом и т.п. с обозначением выносного элемента прописной буквой русского алфавита на полке линии-выноски. Над изображением выносного элемента указывают обозначение и масштаб, в котором он выполнен

Выносной элемент располагают на чертеже возможно ближе к соответствующему месту на изображении предмета.

Построение аксонометрической проекции

В аксонометрии обычно выполняют вырез¼ части детали, при этом вырез не всегда повторяет разрез, выполненный на ортогональном изображении. Угол, образованный секущими плоскостями, должен быть раскрыт.

На рис. 34 – 37 показано поэтапное выполнение изометрии детали с

вырезом ¼ части. Для удобства построений будем считать, что нижняя плоскость детали совпадает с горизонтальной плоскостью проекций, а осьz – с осью конической и цилиндрической поверхностей.

Рис. 34 Рис. 35

Рис. 36 Рис. 37

Выполнение задания начинаем с построения аксонометрических осей и очертания плоских фигур, полученных при сечении детали вертикальными плоскостями, проведенными по осям симметрии детали (рис. 34).

Отмечаем центры окружностей усеченного конуса и цилиндров – точки О1 , О2 , О3 , О4 и строим изометрические проекции тех частей окружностей, которые остались после выполнения выреза (рис. 35). Заканчиваем построение прямоугольных очертаний детали (рис. 36). Выполнив штриховку плоских фигур, образовавшихся при сечении детали вертикальными плоскостями (проводя линии штриховки параллельно направлениям, показанным на рисунке), обводим контур детали (рис. 37).

Построение наклонного сечения

Наклонное сечение получается от пересечения предмета плоскостью, составляющей с горизонтальной плоскостью проекций угол, отличный от прямого.

На чертеже наклонные сечения выполняют по типу вынесенных сечений и в соответствии с направлением, указанным стрелками на линии сечения. При построении сечения не является обязательным строгое соблюдение проекционной связи между изображением, где задан след секущей плоскости, и фигурой сечения. Фигуру сечения можно расположить в любом удобном месте поля чертежа, рис. 38, б, в. При этом, если ориентация сечения на чертеже не соответствует направлению взгляда, указанному стрелками на штрихах линии сечения, то обозначение сечения должно сопровождаться знаком повернуто, рис. 38, в.

Само же задание обычно звучит так: "построить натуральный вид фигуры сечения" . Конечно же, мы решили не оставлять этот вопрос в стороне и постараться по возможности объяснить, как происходит построение наклонного сечения.

Для того, чтобы объяснить, как строится наклонное сечение, я приведу несколько примеров. Начну конечно же с элементарного, постепенно наращивая сложность примеров. Надеюсь, что проанализировав эти примеры чертежей сечений, вы разберетесь в том, как это делается, и сможете сами выполнить свое учебное задание.

Рассмотрим "кирпичика" с размерами 40х60х80 мм произвольной наклонной плоскостью. Секущая плоскость разрезает его по точкам 1-2-3-4. Думаю, тут все понятно.

Перейдем к построению натурального вида фигуры сечения.
1. Первым делом проведем ось сечения. Ось следует чертить параллельно плоскости сечения - параллельно линии, в которую проецируется плоскость на главном виде - обычно именно на главном виде задают задание на построение наклонного сечения (Далее я всегда буду упоминать про главный вид, имея в виду что так бывает почти всегда в учебных чертежах).
2. На оси откладываем длину сечения. На моем чертеже она обозначена как L. Размер L определяется на главном виде и равен расстоянию от точки вхождения сечения в деталь до точки выхода из нее.
3. Из получившихся двух точек на оси перпендикулярно ей откладываем ширины сечения в этих точках. Ширину сечения в точке вхождения в деталь и в точке выхода из детали можно определить на виде сверху. В данном случае оба отрезка 1-4 и 2-3 равны 60 мм. Как видно из рисунка выше, края сечения прямые, поэтому просто соединяем два наших получившихся отрезка, получив прямоугольник 1-2-3-4. Это и есть - натуральный вид фигуры сечения нашего кирпичика наклонной плоскостью.

Теперь давайте усложним нашу деталь. Поставим кирпичик на основание 120х80х20 мм и дополним фигуру ребрами жесткости. Проведем секущую плоскость так, чтобы она проходила через все четыре элемента фигуры (через основание, кирпичик и два ребра жесткости). На рисунке ниже вы можете увидеть три вида и реалистичое изображение этой детали

Попробуем построить натуральный вид этого наклонного сечения. Начнем опять с оси сечения: проведем ее параллельно плоскости сечения обозначенного на главном виде. На ней отложим длину сечения равную А-Е. Точка А является точкой входа сечения в деталь, а в частном случае - точкой входа сечения в основание. Точкой выхода из основания является точка В. Отметим точку В на оси сечения. Аналогичным образом отметим и точки входа-выхода в ребро, в "кирпичик" и во второе ребро. Из точек А и В перпендикулярно оси отложим отрезки равные ширине основания (в каждую сторону от оси по 40, всего 80мм). Соединим крайние точки - получим прямоугольник, являющийся натуральным видом сечения основания детали.

Теперь настал черед построить кусочек сечения, являющийся сечением ребра детали. Из точек В и С отложим перпендикуляры по 5 мм в каждую сторону - получатся отрезки по 10 мм. Соединим крайние точки и получим сечение ребра.

Из точек С и D откладывем перпендикулярные отрезки равные ширине "кирпичика" - полностью аналогично первому примеру этого урока.

Отложив перпендикуляры из точек D и Е равные ширине второго ребра и соединив крайние точки получим натуральный вид его сечения.

Остается стереть перемычки между отдельными элементами получившегося сечения и нанести штриховку. Должно получиться что-то вроде этого:

Если же по заданному сечению произвести разделение фигуры, то мы увидим следующий вид:

Я надеюсь, что вас не запугали нудные абзацы описания алгоритма. Если вы прочли все вышенаписанное и еще не до конца поняли, как начертить наклонное сечение , я очень советую вам взять в руки лист бумаги и карандаш и попытаться повторить все шаги за мной - это почти 100% поможет вам усвоить материал.

Когда-то я пообещал продолжение данной статьи. Наконец-то я готов представить вам пошагового построения наклонного сечения детали, более приближенной к уровню домашних заданий. Более того, наклонное сечение задано на третьем виде (наклонное сечение задано на виде слева)

или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение.

Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое на более сложной детали, с фасками и конусовидным отверстием например.

Спасибо. А разве на разрезах ребра жесткости не штрихуются?
Именно. Именно они и не штрихуются. Потому что таковы общие правила выполнения разрезов. Однако их обычно штрихуют при выполнении разрезов в аксонометрических проекциях - изометрии, диметрии и т.д. При выполнении наклонных сечений, область относящаяся к ребру жесткости так же заштриховывается.

Спасибо,очень доступно.Скажите,а наклонное сечение можно выполнить на виде с верху,или на виде слева?Если да,то хотелось бы увидеть простейший пример.Пожалуйста.

Выполнить такие сечения можно. Но к сожалению у меня сейчас нет под рукой примера. И есть еще один интересный момент: с одной стороны, там ничего нового, а с другой стороны на практике такие сечения чертить реально сложнее. Почему-то в голове все начинает путаться и у большинства студентов возникают сложности. Но вы не сдавайтесь!

Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое, но с отверстиями (сквозными и несквозными), а то в элипс они в голове так и не превращаются

помогите мне по комплексной задаче

Жаль, что вы именно тут написали. Написали бы в почту - может мы смогли бы успеть все обсудить.

Хорошо объясняете. Как быть если одна из сторон детали полукруглая? А также в детали есть отверстия.

Илья, используйте урок из раздела по начертательной геометрии "Сечение цилиндра наклонной плоскостью". С его помощью сможете разобраться, что делать с отверстиями (они же по сути тоже цилиндры) и с полукруглой стороной.

благодарю автора за статью!кратко и доступно пониманию.лет 20 назад сам грыз гранит науки,теперь сыну помогаю. многое забыл,но Ваша статья вернула фундаментальное понимание темы.Пойду с наклонным сечением цилиндра разбираться)

Добавьте свой комментарий.